Expliciter cette suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 20 Avr 2013, 12:42
par upium666 » 20 Avr 2013, 12:42
Bonjour à tous et à toutes !
_{n \in \mathbb{N}} : \left\{\begin{matrix} u_0=a \in \mathbb{R}^* \\ u_{n+1}=\frac{1}{u_n} \end{matrix}\right.)
Exprimer

en fonction de

et

Merci
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 20 Avr 2013, 12:53
par upium666 » 20 Avr 2013, 12:53
Voici ce que j'ai trouvé :

^n)
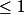
^n+1 \leq 2)
^n+1}{2} \leq 1)
(\frac{(-1)^n+1}{2}) \leq a-\frac{1}{a})
(\frac{(-1)^n+1}{2}) \leq a)
On définit alors :
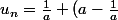(\frac{(-1)^n+1}{2}))
Mon professeur m'a dit que c'est faux à partir de la 4ème ligne (et il a raison) car je n'ai pas pris en compte que
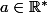
et donc que
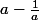
peut être négatif, ce qui changerait l'encadrement
Cependant ...
Il s'avère que ça marche ! :doh:
C'est pour cela que je demanderais votre aide
Merci ! :we:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Avr 2013, 13:28
par Nightmare » 20 Avr 2013, 13:28
Salut,
comment de ton encadrement déduis-tu le terme général de la suite?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 20 Avr 2013, 13:34
par Ericovitchi » 20 Avr 2013, 13:34
Tu te compliques un peu la vie. Regarde simplement les premiers termes de ta suite et devine que
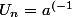^n})

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 20 Avr 2013, 13:35
par Lostounet » 20 Avr 2013, 13:35
Bonsoir,
Pour n pair, Un = a
Pour n impair, Un = 1/a !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 20 Avr 2013, 14:05
par upium666 » 20 Avr 2013, 14:05
Ericovitchi a écrit:Tu te compliques un peu la vie. Regarde simplement les premiers termes de ta suite et devine que
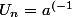^n})
C'est vrai, c'est tout bête :p
Merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités