bijour!
pouvez vous m'expliquer par étapes détaillées la forme canonique de cette expression:
P(x)=ax²+bx+c
mettez pleins d'explications à chaque fois que vous faites une étape svp car je suis perdue:'(.
Merci.
Explication de la forme canonique.
4 messages
- Page 1 sur 1
par fonfon » 27 Sep 2006, 15:31
Salut pour trouver la forma canonique d'un polynôme du second degré on utilises les identitées remarquables
}=ax^2+bx+c)
}=a(x^2+\frac{bx}{a}+\frac{c}{a}))
dans la parenthése ont fait apparaitre un carré auquel il faut retranché ce qu'il y a en trop pour avoir toujours la bonne forme de f(x) soit
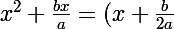^2-(\frac{b}{2a})^2)
donc
}=a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{c}{a}))
soit en reduisant au m^me denominateur on obtient:
}=a((x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a^2}))
voilà c'est la formule pour la forme canonique
dans la parenthése ont fait apparaitre un carré auquel il faut retranché ce qu'il y a en trop pour avoir toujours la bonne forme de f(x) soit
donc
soit en reduisant au m^me denominateur on obtient:
voilà c'est la formule pour la forme canonique
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :