Salut!!
je me suis bloké dans cette question de trigo!!je voudrais bien que quelqu'un m'aide!! Merci d'avance!!
exo:
developper puis transformer en produit l'expression
Sin²a+ sin²b- sin²(a+b)
Merci d'avance!!
Exo!! Trigo: un ptit probléme
10 messages
- Page 1 sur 1
re:trigo:un ptit probleme
par dom85 » 26 Oct 2005, 21:57
bonsoir,
sin(a+b)=sina cosb+sinb cosa
sin²(a+b)=sin²a cos²b+2sina sinb cosa cosb+sin²bcos²a
tu obtiens:
sin²a+sin²b-sin²acos²b-sin²bcos²a-2sina sinb cosa cosb=
sin²a(1-cos²b)+sin²b(1-cos²a)-2sina sinb cosa cosb=
sin²a sin²b+sin²b sin²a-2 sina sinb cosa cosb=
2sina sinb(sina sinb-cosa cosb)
bonne soirée
sin(a+b)=sina cosb+sinb cosa
sin²(a+b)=sin²a cos²b+2sina sinb cosa cosb+sin²bcos²a
tu obtiens:
sin²a+sin²b-sin²acos²b-sin²bcos²a-2sina sinb cosa cosb=
sin²a(1-cos²b)+sin²b(1-cos²a)-2sina sinb cosa cosb=
sin²a sin²b+sin²b sin²a-2 sina sinb cosa cosb=
2sina sinb(sina sinb-cosa cosb)
bonne soirée
par Malek » 26 Oct 2005, 22:08
Merci bien !! mais je vais vous deranger encore un peu!!
car on me demande de commencer par utiliser la fotmule suivante!!
Sin²x=
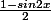
Alors comment faire!!
et encore une fois Merci BCP
car on me demande de commencer par utiliser la fotmule suivante!!
Sin²x=
Alors comment faire!!
et encore une fois Merci BCP
par danskala » 26 Oct 2005, 22:13
Malek a écrit:on me demande de commencer par utiliser la fotmule suivante!!
Sin²x=
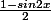
Que veux-tu dire exactement?
Quel est l'énoncé précis de la question ?
par Malek » 26 Oct 2005, 22:18
l'enoncé est ça:
exo:
developper puis transformer en produit l'expression
Sin²a+ sin²b- sin²(a+b)
Mais le professeur nous a demandé d'utiliser pour le developpement la formule Sin²x
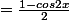
Ok??
exo:
developper puis transformer en produit l'expression
Sin²a+ sin²b- sin²(a+b)
Mais le professeur nous a demandé d'utiliser pour le developpement la formule Sin²x
Ok??
par danskala » 26 Oct 2005, 23:05
C'est peut-être cela, mais c'est plus compliqué que la 1ère méthode:
Notons f(a,b) ton expression.
On a, en se servant de la formule de ton prof:
=\frac{1-cos 2a}{2}+\frac{1-cos 2b}{2}-\frac{1-cos 2(a+b)}{2})
=\frac{1-cos 2a-cos 2b+cos (2a+2b)}{2})
=\frac{1-cos 2a-cos 2b+cos2a\cos2b-sin2a\sin2b}{2})
=\frac{(1-cos 2a)(1-cos 2b)-sin2a\sin2b}{2})
Avec la formule de ton prof on a
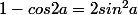
et 
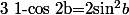
donc
=\frac{2sin^2a\times 2sin^2b-sin2a\sin2b}{2})
=\frac{4sin^2a\sin^2b-2sinacosa\times 2sinbcosb}{2})
(
)
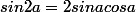
=2sin^2a\sin^2b-2sinacosasinbcosb)
=2sinasinb(sinasinb-cosacosb))
Et là on retombe sur la fin du calcul de la première méthode
Voilà
bye
:we:
Notons f(a,b) ton expression.
On a, en se servant de la formule de ton prof:
Avec la formule de ton prof on a
Et là on retombe sur la fin du calcul de la première méthode
Voilà
bye
:we:
par Malek » 27 Oct 2005, 22:18
dsl je vous derange encore un peu !! si je travaille comme ça !! est ce que c'est juste???
=\frac{1-cos 2a}{2}+\frac{1-cos 2b}{2}-(1-cos^2(a+b)))
=\frac{2-cos 2a-cos 2b}{2}-1+cos^2(a+b))
=\frac{2-(cos 2a+cos 2b)}{2}-1+cos^2(a+b))
=\frac{2-2 cos(a+b)cos(a-b)}{2}-1+cos^2(a+b))
=1-cos(a+b)cos(a-b)-1+cos^2(a+b))
=cos(a+b) [cos(a+b)-cos(a-b)])
=cos(a+b) [-2 sin(a)* sin(b)])
=-2 cos(a+b)*sin(a)*sin(b))
Merci
Merci
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :