Exo
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 08 Oct 2014, 23:57
par hazal_kaya » 08 Oct 2014, 23:57
[img]960×576[/img]
avez vs des idées .! Je me suis bloquée à 2
-
mathelot
 par mathelot » 09 Oct 2014, 06:10
par mathelot » 09 Oct 2014, 06:10
l'image ne s'affiche pas.
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 09 Oct 2014, 14:00
par hazal_kaya » 09 Oct 2014, 14:00
D acc je vais ecrire l exercice
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 09 Oct 2014, 15:11
par hazal_kaya » 09 Oct 2014, 15:11
F continue sur [a.b] vers [a.b]
;)x;)[a,b] : f;)f(x)=x
on pose l'ensemble E :
E=(x;)[a,b]; f(x)=x)
1- montrer que E;);)
2-montrer que E=f([a,b])
3-montrer que E ;) ;)
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 09 Oct 2014, 15:16
par hazal_kaya » 09 Oct 2014, 15:16
voila ce que j ai fait pour 2 :
f([a,b])=(f(x), x;) [a,b])
on pose y ;) E
y;) E => f(y) = y
=> y ;) f ([a,b])
=> E ;) f([a,b])
mais je dois trouver que f([a,b]) ;) E et là je me suis bloquée
-
mathelot
 par mathelot » 09 Oct 2014, 15:20
par mathelot » 09 Oct 2014, 15:20
hazal_kaya a écrit:f continue sur [a.b] vers [a.b]

x;)[a,b] : f;)f(x)=x
on pose l'ensemble E :
E=(x;)[a,b]; f(x)=x)
1- montrer que E;);)
2-montrer que E=f([a,b])
3-montrer que E


bonjour,
indicationspour montrer
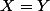
on montre
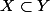
puis
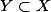
 \geq a)
et .....
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 09 Oct 2014, 15:25
par hazal_kaya » 09 Oct 2014, 15:25
oui c est ce que je veux faire pour la démontrer !!
-
mathelot
 par mathelot » 09 Oct 2014, 16:17
par mathelot » 09 Oct 2014, 16:17
Que peut on dire de f(b) ?
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 09 Oct 2014, 18:17
par hazal_kaya » 09 Oct 2014, 18:17
Entre a et b

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Oct 2014, 23:19
par Ben314 » 09 Oct 2014, 23:19
hazal_kaya a écrit:F continue sur [a.b] vers [a.b]

x;)[a,b] : f;)f(x)=x
on pose l'ensemble E :
E=(x;)[a,b]; f(x)=x)
1- montrer que E;);)
2-montrer que E=f([a,b])
3-montrer que E


Y'a deux trucs qui m'échappent :
2- Il me semble bien que f:[0,1] -> [0,1] ; x -> 1-x vérifie les hypothèses et que pourtant E={1/2} est différent de f([0,1])=[0,1]
3- Je vois pas trop l'intérêt de la question... :hum:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 10 Oct 2014, 12:50
par mathelot » 10 Oct 2014, 12:50
hazal_kaya a écrit:f continue sur [a.b] vers [a.b]

x;)[a,b] : f;)f(x)=x
on pose l'ensemble E :
E=(x;)[a,b]; f(x)=x)
1- montrer que E;);)
2-montrer que E=f([a,b])
3-montrer que E


1.
 \geq a)
 \leq b)
-x)
s'annule par continuité sur [a;b]
2. si

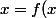)
donc
)
réciproque fausse.
ce qui serait "intéressant" ,c'est un exo qui comparerait les points fixes de

et les points fixes de

,etc..
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 10 Oct 2014, 14:49
par hazal_kaya » 10 Oct 2014, 14:49
Non je veux commencer par x appartient à f([a.b]) et trouver que x appartient à E
-
mathelot
 par mathelot » 10 Oct 2014, 16:20
par mathelot » 10 Oct 2014, 16:20
Ben314 a indiqué un contre-exemple.
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Oct 2014, 17:39
par paquito » 10 Oct 2014, 17:39
on a fof(a)=a et fof(b)=b et fof(x)-f(x)=0, donc il existe af(a) et fof(c)a et f(c)fof(x)=x <=> f(x)=f(x), ce qui n'est pas une surprise! Après je ne comprends pas l'intérêt de la question puisque E inclus dans R est une vérité de la Palice!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
x;)[a,b] : f;)f(x)=x

x;)[a,b] : f;)f(x)=x

