Exo suites démonstration par récurrence

[thisisme]

[FONT=Arial]bonjour j'ai un exo pour lundi de révision , j'ai du faire ce genre de choses l'année précédente mais je ne retrouve pas mon cahier :triste: et je n'arrive pas le résoudre :mur: :

Soit la suite u définie par U0=0 et pour tout entier naturel n, Un+1=1/(2-Un).

1) démontrer par récurrence que pour tout entier naturel n, Un<1. En déduire que la suite u est bien définie.

2) Calculer les 4 premiers termes de la suites u. Conjecturer une expression de Un en fonction de n puis la démontrer.

merci de m'aider et m'expliquer le raisonnement [/FONT]

[C.Ret]

Bonsoir.

Ne perdons pas de temps, où est-ce que ça bloque ?

[ampholyte]

Bonjour,

1) Ton hypothèse de récurrence est "la suite Un < 1 pour tout n"
La démonstration par récurrence se démontre en 3 étapes


Etape 1 : Initialisation
Tu vérifies que Uo est bien inférieur à 1

Etape 2 : Généralisation
Tu supposes que Un < 1, tu calcules Un+1 à partir de la formule que tu as, tu vérifies que Un+1 < 1

Etape 3: Conclusion
Comme Uo est vrai et que si Un < 1 alors Un+1 < 1, par récurrence la suite Un < 1 pour tout n

2) Le calcul des 4 premiers termes revient à calculer U1, U2, U3, U4 (ou si tu préfères pour n= 0, n = 1, n = 2, n = 3)

Conjecturer une expression signifie que tu dois trouver une expression qui semble fonctionner pour les premiers termes. Il faudra ensuite que tu la démontres (par récurrence)

Si tu as d'autres questions n'hésite pas

[thisisme]

[FONT=Arial]Je bloque pour démontrer par récurrence que Un<1[/FONT]

[C.Ret]

ampholyte vient de suggérer un cheminement qui me parait bien adapté.

En plus, est-ce que tu vois pourquoi montrer que u(n)<1 pour tout n est important car cela prouve que la suite est définie ?

[thisisme]

[FONT=Arial]oui ok merci j'ai compris pour la question 1
[/FONT]

[thisisme]

[FONT=Arial]par contre pour calculer Un+1 comment je fais? je fais U0+1=1/-2-U0)=1/2? c'est ca?[/FONT]

[ampholyte]

[FONT=Arial]par contre pour calculer Un+1 comment je fais? je fais U0+1=1/-2-U0)=1/2? c'est ca?[/FONT]

Regarde c'est pas si compliqué.

Tu pars de ton hypothèse Un -1 (on multiplie par -1 donc on change l'inégalité)
2-Un > 2-1
2-Un > 1
1/(2-Un) On a prouvé que Un+1 < 1 si Un < 1

As-tu compris cette étape maintenant ?

[thisisme]

[FONT=Arial]merci et donc après pour la question deux pour calculer U1 je fais U0+1=U1=1/(2-U0)=1/2 C'est ca??? et je fais pareil pour U2, U3 et U4
[/FONT]

[ampholyte]

[FONT=Arial]merci et donc après pour la question deux pour calculer U1 je fais U0+1=U1=1/(2-U0)=1/2 C'est ca??? et je fais pareil pour U2, U3 et U4
[/FONT]

Tout à fait

[C.Ret]

[FONT=Arial]merci et donc après pour la question deux pour calculer U1 je fais U0+1=U1=1/(2-U0)=1/2 C'est ca??? et je fais pareil pour U2, U3 et U4
[/FONT]

Ben non, l'énoncé dit que la suite est définie par u_0=0 et

Donc mais ça ne mène à rien.

Par contre, cela signifie que pour calculer tu utilise la formule avec .



Je te laisse continuer.
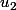
Une fois calculé, tu peux calculer et ansi de suite.

[thisisme]

[FONT=Arial]merci beaucoup de m'avoir aidé grace à toi j'ai réussi a faire cet exercice :we: [/FONT]

[C.Ret]

[quote="thisisme"][COLOR=DarkSlateBlue][SIZE=3][FONT=Arial]merci beaucoup de m'avoir aidé Ah! Très bien.

Je suis curieux, quelle formule as-tu conjecturée pour définir le terme général de la suite ?

[thisisme]

[FONT=Arial Black]donc U1=1/2, U2=2/3, U3=3/4 et U4=4/5[/FONT]

[thisisme]

[FONT=Arial Black]et donc Un=n/(n+1)[/FONT]

[thisisme]

[FONT=Arial]c'est bon pour Uo et encore une fois je n'arrive pas à le montrer pour Un+1
[/FONT]

[C.Ret]

Non c'est juste.

Pour démontrer la conjecture, on le fait come pour montre la limite, on le fait par récurrence.

On vérifie pour ou pour .
Ca colle

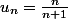
Puis on fait l'hypothèse que et on calcule

D'après la définition
On remplace u_n dans l'expression de u_{n+1} par notre formule conjecturée :

Et là on simplifie l'expression en espérant arriver au rapport attendu :


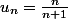
Donc, on a montré que si alors la relation est vérifiée égalemetn pour .
Et comme on l'a vérifié pour u_0 c'est vrai pour tout n.
La formule conjecturée est bien l'expression générale de la suite.

On vérifie de plus que

[thisisme]

[FONT=Arial]encore merci pour tout à vous deux c'est bon[/FONT]