Un exo ou je n ai rien compris

[killik2023]

c'est des exos a faire pour s'entrainer car on a un controle a la rentrée . mais celui la me pose des problemes,donc si vous pouviez maider. :id:

On desire cloturer un terrain rectangulaire de 400m2 en utilisabbt le moin de grillage possible .on souhaite determiner la longeur du grillage minimale necessaire.soit x ety les dimensions de cotes du rectangle.

1 quelle relation lie x et y?
2 on note P(x) le demi perimetre du terrain en fonction de x
montre que P(x)= x+400/x

3 montrer que pour tout x superieu ou egale a 0: x+400/x est superieur ou egale a 40

4 en deduire que al fonction p admet un minimum sur [0;+ infini[

5 repondre au problem pose
:triste: :triste: :triste: :triste:

[allomomo]

Salut,


1 - L'air d'un rectangle est :
2 - D'après 1) on a . Or le périmètre d'un rectangle s'écrit : 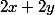, le moitié de ce périmètre est, donc, nécessairement
3 - Pour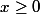 on a Ce qui est vrai tout le temps. Donc on a ce qu'on cherche.

4 - on cherche un minimum tel que sur [0, +inf[ (voir3))
Min atteind en x=20 et vaut 40. sur [0, +inf[ (et admet un max sur ]-inf, 0] en x=-20 et vaut -40)

[The Void]

1) quelles est la formule pour trouver l'aire d'un rectangle?

2)Le périmètre total est 2x+2y donc P(x)=x+y et tu remplace y en utilisant l'expression trouvée en 1)

3) je suppose que x est superieur strictement à 0 et pas superieur ou egal... car x+400/x n'existe pas pour x=0
sinon il faut faire x+400/x >= 40
x+400/x-40 >= 0
(x²+400-40x)/x >= 0
calcul du discriminant, tableau de variation, tu trouves ainsi que le minimum est atteint pour x=20, ce qui correspond à P(x)=40, x+400/x est dc bien supérieur à 40

4) minimum en x=20

5) Comme p(x) représente la moitié du grillage, le minimum de grillage est donc 20*2=40

edit: oups, un peu à la bourre

[killik2023]

Salut,


1 - L'air d'un rectangle est :
2 - D'après 1) on a . Or le périmètre d'un rectangle s'écrit : , le moitié est, donc, nécessairement
3 - Pour on a Ce qui est vrai tout le temps. Donc on a ce qu'on cherche.

ok merci pour le coup de main mais tu a oublie un mot je crois apre, le moitié est , donc ,ect

[killik2023]

1) quelles est la formule pour trouver l'aire d'un rectangle?

2)Le périmètre total est 2x+2y donc P(x)=x+y et tu remplace y en utilisant l'expression trouvée en 1)

3) je suppose que x est superieur strictement à 0 et pas superieur ou egal... car x+400/x n'existe pas pour x=0
sinon il faut faire x+400/x >= 40
x+400/x-40 >= 0
(x²+400-40x)/x >= 0
calcul du discriminant, tableau de variation, tu trouves ainsi que le minimum est atteint pour x=20, ce qui correspond à P(x)=40, x+400/x est dc bien supérieur à 40

4) minimum en x=20

5) Comme p(x) représente la moitié du grillage, le minimum de grillage est donc 20*2=40

edit: oups, un peu à la bourre

lol dsl je nai pas compris quand tu ecris , calcul du descrminant