c'est pas vraiment malin de virer des messages :hum:
ensuite c'est pas grave de comettre des erreur le pire c'est de persister en erreur !
bon reprenons dés le début , je crois que tu as un problème avec la définition :
on a
 dt = \left[F(t)\right]_a^b = F(b)-F(a))
on est d'accord ?
ensuite on a :
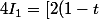e^{\frac{t}{2}\right]_0^1 - (-2 \int_0^1 e^{\frac{t}{2}} dt ) = \left[2(1-t)e^{\frac{t}{2}\right]_0^1 + 2 \left[2e^{\frac{t}{2}\right]_0^1 = ( 0 - 2(1-0)e^0 ) + 2(2e^{\frac{1}{2}}-2e^0) = -2 + 4e^{\frac{1}{2}} - 4 = -6 +4 e^{\frac{1}{2}})
donc
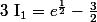
d'ailleurs le résultat que tu cherche à démontrer aprés affirme ce résultat :
on te demande de mq :
!})
donc essaie avec n=0 , tu dois trouver
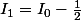
et c facile de calculer
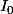
sinon pour démonter cette relation tu utilise comme d'hab une ipp .
tu as :
!)I_{n+1} = \int_0^1 (1-t)^{n+1} e^{\frac{t}{2}}dt)
tu fais donc une ipp en posant
 = (1-t)^{n+1})
et
= e^{\frac{1} {2}})
et ça coule ....