[TS] Exo Intégrales-Suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
LeFish
- Membre Relatif
- Messages: 330
- Enregistré le: 23 Nov 2008, 16:16
-
 par LeFish » 27 Jan 2009, 19:30
par LeFish » 27 Jan 2009, 19:30
Bonsoir à tous !
J'ai besoin d'aide comme vous pouvez vous en douter :
Démontrer que
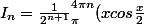dx)
est une suite géométrique de raison q .
En posant
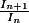
, on arrive à
\pi}(xcos\frac{x}{2})dx)
.
En intégrant par parties et en utilisant les formules d'addition , j'arrive à
)
, mais ça m'aide pas vraiment puisqu'on doit trouver q constant ^^.
Donc si vous pouviez m'indiquer comment faire , ca serait bien sympathique ( juste des petites astuces bien sur . )
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 27 Jan 2009, 20:01
par Nightmare » 27 Jan 2009, 20:01
Bonsoir,
Comment as-tu calculé ton quotient d'intégrales?
Plutôt écrire que :
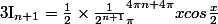dx=\frac{1}{2}I_{n}+\frac{1}{ 2^{n+2}}\Bigint_{4\pi n}^{4\pi (n+1)} xcos\(\frac{x}{2}\)dx)
En posant
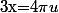
le deuxième terme devient :
du)
et il te reste à montrer que ce truc là est nul.
-
bibounette
- Membre Naturel
- Messages: 10
- Enregistré le: 27 Jan 2009, 13:27
-
 par bibounette » 27 Jan 2009, 20:04
par bibounette » 27 Jan 2009, 20:04
Bonjour ,pour ton integrales ta pa besoin de passer par I(n+1)/I(n) , tu peux simplement faire une integrale par partie en pose U=COS(X/2) et V=X
ensuite aprés avoir fais ton intégration tu va trouver:
In=1/2^(n+1)-2pi+cos(2pi*n)-cos(pi/2)).
Les cos vont partir car c'est depuis periodique. ainsi ta une suite geometrique tel que
In=(-pi+2)*(1/2)^n
-
LeFish
- Membre Relatif
- Messages: 330
- Enregistré le: 23 Nov 2008, 16:16
-
 par LeFish » 27 Jan 2009, 20:30
par LeFish » 27 Jan 2009, 20:30
Nightmare , je sais pas comment t'as pu " enlever " les 4

en haut et en bas de l'intégrale et à gauche du
)
, une propriété que je conaissais pas ^^.
Pour le quotient d'intégrales j'ai utilisé la relation de Chasles pour trouver une intégrale de

à
)
de xcos(x/2)dx ( le tout fois 1/2 ( ce qui correspond à ce que j'ai dis au début )
Et Bibounette , j'ai direct integré par parties , mais j'trouve pas comme toi ^^.
J'trouve que
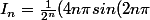+2cos(2n \pi)-\pi))
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 27 Jan 2009, 20:37
par Nightmare » 27 Jan 2009, 20:37
Oui désolé, j'ai utilisé un changement de variable mais ce n'est plus au programme de terminale.
Tu parles de la relation de Chasles, il ne me semble pas qu'elle s'applique pour un quotient !
-
bibounette
- Membre Naturel
- Messages: 10
- Enregistré le: 27 Jan 2009, 13:27
-
 par bibounette » 27 Jan 2009, 20:50
par bibounette » 27 Jan 2009, 20:50
alors prend simplement l'integrale.
on considere , U'=cos(x/2) U=2sin(x/2)
V=x V'=1
alors la tu a =[2xsin(x/2)]-integrale(2sin(x/2))
or integrale(2sin(x/2))-2[-2cos(x/2)]=-2pi*1 + 4(1-0)=-2pi+4
voila ce ki fau trouver .
et quand tu devellope par raport au borne tu trouve ce ke jai trouver .
de plus , sin(2pi(n))=0 et cos(2pi(n))=1
stp comment tu fai pr avoir les formules maths des integrales enfin tout l'outils mathematique , pck je galere pr ecrire
-
LeFish
- Membre Relatif
- Messages: 330
- Enregistré le: 23 Nov 2008, 16:16
-
 par LeFish » 27 Jan 2009, 21:21
par LeFish » 27 Jan 2009, 21:21
Quand tu dis qu'il faut trouver

, c'est quand t'as posé n=0 , parce que pour trouver

, faut avoir 0 et

comme bornes , alors que dans l'exo c'est

et

.^^
Et surtout pour les belles formules , tu clique sur "TEX" ( juste au dessus de là ou t'écris ) , et tu va voir sur ce topic :
http://maths-forum.com/showthread.php?t=70548 pour les formules.
-
bibounette
- Membre Naturel
- Messages: 10
- Enregistré le: 27 Jan 2009, 13:27
-
 par bibounette » 27 Jan 2009, 21:24
par bibounette » 27 Jan 2009, 21:24
non il faut que tu sache ke la fonction cosinus et 2

periodique c a d que quelque soit n appartenant a ensemble des entier naturelle , on a toujours cos(2

n)=1 et sinus quelque soit n , on a sinus(2

n)=0
-
LeFish
- Membre Relatif
- Messages: 330
- Enregistré le: 23 Nov 2008, 16:16
-
 par LeFish » 27 Jan 2009, 21:36
par LeFish » 27 Jan 2009, 21:36
Ah je savais pas pour les
=1)
et sin(2\pi n)=0 , effectivement c'est très utile , merci beaucoup ! :we:
( Ps : change le sens de ta barre , pour pi c'est \ et non / ( pour beaucoup de formules d'ailleurs ... )
Et donc je trouve bien ce que t'as trouvé au début \o/ danke schön !
Merci aussi à Nightmare qui m'a aidé même s'il m'a pas vraiment aidé , en tout cas je saurai un truc de Prépa :zen:
-
bibounette
- Membre Naturel
- Messages: 10
- Enregistré le: 27 Jan 2009, 13:27
-
 par bibounette » 27 Jan 2009, 21:37
par bibounette » 27 Jan 2009, 21:37
regarde si tu considere n=7 (impaire par exemple)
cos(7*2*

)=cos(14

)=cos(2

)=1 car 2

periodique
si tu considere n =10(pairs)
cos(10*2*

)=cos(2*

)=1
de meme pr sinus tjr egale a 0 car sinus(2*

)=0
-
LeFish
- Membre Relatif
- Messages: 330
- Enregistré le: 23 Nov 2008, 16:16
-
 par LeFish » 27 Jan 2009, 21:40
par LeFish » 27 Jan 2009, 21:40
Effectivement oui c'est plutôt " bete " , merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
