Exo complexe

[Phile]

Bonjour,

Je bloque sur l'exercice suivant :

On donne 3 points A, B, C d'affixes a,b,c non nulles et 3 points P,Q,R d'affixes p,q,r avec p=|a|/a, q=|b|/b et r=|c|/c.
Soit H le point défini par Vect(OH)=Vect(OP)+Vect(OQ)+Vect(OR).
Il faut montrer que H est l'orthocentre du triangle PQR (j'ai tenté un produit scalaire sans succès) et que le triangle PQR est équilatéral ssi p+q+r=0

Vous remerciant par avance

[Ericovitchi]

oui calcules les affixes de PH, QH et RH
Celle de PH par exemple c'est |b|/b+|c|/c et donc PH=OQ+OR (vectoriellement)
Pour montrer que H est orthocentre, il faut que tu montres que PH est perpendiculaire à QR
Formes le produit scalaire PH.QR=(OQ+OR)(OR-OQ)=OR²-OQ²=1-1=0
C'est donc bien le cas

[Phile]

Merci à toi Ericovitchi,

Effectivement, la réponse est très simple, je n'avais pas remarquer que |p|=|q|=|r|=1.
Est-ce que tu as une idée pour la deuxième question, j'ai transformé les distances en module, j'ai essayé d'exprimer les égalités avec les conjugués mais je ne parviens pas à l'égalité demandée.

je cherche...

[Ericovitchi]

Si tu prends 3 points sur un cercle trigonométrique de rayon 1 (PQR), pour qu'ils forment un triangle équilatéral, il faut qu'il soient déduits des points 1, j ,j² par une rotation d'angle theta donc que p=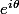 q= et r=et ça entraîne bien que p+q+r=0 (car 1+j+j²=0)

réciproquement, si p+q+r=0 démontres que ça entraîne que le triangle est équilateral

[Ericovitchi]

En y réfléchissant, ça revient en fait à démontrer que le triangle PQR est équilatéral si et seulement si son orthocentre H et le centre O de son cercle circonscrit sont confondu (ce qui est assez évident car si les hauteurs et les médiatrice sont confondues ça entraîne l'égalité des cotés).

Voici un lien qui parle de cette question.

Rigolo comme exercice car on en déduit finalement que si 3 angles sont tels que la somme de leur cosinus et la somme de leur sinus est nulle alors ces 3 angles diffère de 2pi/3. Pas forcement facile à démontrer directement.

PS. Il y a un truc qui me trouble. En faisant ces calculs, je suis aussi tombé sur le fait que p-q=-j²(r-q) (on exprime la rotation de 60°) qui peut s'écrire p+jq+j²r=0 ce qui dans mon souvenir était la vraie formule pour caractériser un triangle équilatéral avec des nombres complexes. Vous pensez que les deux formules sont vraies : p+q+r=0 et p+jq+j²r=0 ? C'est curieux qu'il y ait 2 formules pour caractériser un triangle équilatéral avec des affixes.
Si quelqu'un peut confirmer ou infirmer les deux formules ?

[Phile]

merci pour ton aide, par contre pour démontrer la réciproque, partant de p+q+r=0, j'en déduis que OP+OQ+OR=0 (vectoriellement) et donc que O est le centre de gravité du triangle, qui est alors confondu avec le centre du cercle circonscrit au triangle PQR. J'en conclus alors que le triangle est au moins isocèle, mais comment démontrer qu'il est équilatéral ?

[Ericovitchi]

la démonstration est symétrique en P Q R donc si tu as démontré qu'il était isocèle (par exemple PQ=PR), il l'est aussi avec deux autres sommets (par exemple PR=QR) et donc les 3 cotés sont égaux