Existance de la fonction exponentielle

[Anonyme]

Bonjour,

J'ai une question concernant ce TP:
http://pagesperso-orange.fr/gilles.costantini/Lycee_fichiers/CoursT_fichiers/expeuler.pdf

Dans la Première partie l'auteur suppose que la fonction qu'on recherche existe. Il demande d'admettre cela et dans le parataxe de la page 1 il signale que la démonstration sera faite ultérieurement:en effet, la démonstration de l'existence de la fonction exponentielle se trouve dans un autre cours.

Pourtant dans la 2eme partie: la représentation graphique de la fonction , en utilisant la méthode de euler il arrive a la relation: lorsque

Pourquoi cette égalité ne démontre pas l'existence de la fonction ?
Trouver une forme explicite de la fonction ne demontre - t-elle pas son existence ?

Merci

[benekire2]

c'est quoi l'écriture explicite de la fonction exponentielle pour toi ?

[benekire2]

il utilise simplement des suites adjacentes pour montrer l'existence de la fonction exp,

[Anonyme]

il utilise simplement des suites adjacentes pour montrer l'existence de la fonction exp,

Oui j'ai vu.

Mais dans le TP il arrive a prouver que
et donc en trouvant cela n'a t-il pas demontrer que existe ?
Je pense que oui mais le fait qu'il a dit qu'il démontrera l'existence de exp(x) plus tard avec les suites adjacente me fait douter.

[benekire2]

c'est pas très propre ; ce sont des approximations, normal il construit la courbe.

[Anonyme]

c'est pas très propre ; ce sont des approximations, normal il construit la courbe.

Mais si on fait tendre n a l'infini l'approximation devient une égalité. non ?

Donc je ne vois pas en quoi ce TP ne constitue pas une preuve de l'existence de exp(x).

[benekire2]

sauf que la preuve ca prouve justement que la suite converge vers exp. C'est pas aussi facile que ca de passé à la limite la dessus.

[Anonyme]

sauf que la preuve ca prouve justement que la suite converge vers exp. C'est pas aussi facile que ca de passé à la limite la dessus.

Pourquoi ?

[benekire2]

Ba écrit ta preuve rigoureusement. Après je ne l'ai pas fait depuis quelques temps mais la fois ou je l'avais fait j'étais passé par les adjacentes. Donc si tu y arrive autrement tant mieux.

[Nightmare]

Ba écrit ta preuve rigoureusement. Après je ne l'ai pas fait depuis quelques temps mais la fois ou je l'avais fait j'étais passé par les adjacentes. Donc si tu y arrive autrement tant mieux.

Te ne sembles pas beaucoup te rappeler des preuves que tu as déjà faites dans le passé :lol3:

Qmath > Dans ce TP, la fonction exponentielle est définie comme la solution de l'équation différentielle y'=y avec la condition initiale y(0)=1. A ce moment là et à ce niveau là, on ne peut qu'admettre l'existence d'une solution à cette équadiff et montrer qu'ensuite, si elle existe, elle coïncide avec la fonction .

Bien entendu, on peut faire l'inverse, c'est à dire définir l'exponentielle comme cette dernière limite (dans ce cas, on assure l'existence) et montrer qu'alors elle vérifie l'équadiff de départ. Ce n'est pas le chemin employé ici.

[Anonyme]

si elle existe, elle coïncide avec la fonction .

Merci Nightmare et Benekire.

C'est ce que je cherchais.

Pour la preuve de l'existence avec les suite adjacente je verrai cela demain. Mais je viens de jeter un coup d'oeil rapide sur la demo et il me semble que dans la demo il n'utilise qu'une seule suite non ?

[benekire2]

Te ne sembles pas beaucoup te rappeler des preuves que tu as déjà faites dans le passé :lol3:

ba on peut pas se souvenir en détail de toutes les preuves ... mais bon, je les retrouves vite donc ça passe ..

Qmath--> de rien.
sinon il y en a bien deux de suites je te confirme.

[Nightmare]

C'est pour cela qu'une démonstration, il ne faut pas se contenter de comprendre ce qu'elle dit, mais essayer de comprendre d'où elle vient ! On retient beaucoup mieux une démonstration dont on a compris le fond plutôt qu'une démonstration dont on a vu que la forme :lol3:

[Anonyme]

C'est pour cela qu'une démonstration, il ne faut pas se contenter de comprendre ce qu'elle dit, mais essayer de comprendre d'où elle vient ! On retient beaucoup mieux une démonstration dont on a compris le fond plutôt qu'une démonstration dont on a vu que la forme :lol3:

Par exemple ?
Dans notre cas comment appliquer ton conseil ?

[Nightmare]

Ici, les suites adjacentes stipulées par Benekire ne viennent pas de nulle part mais de la méthode d'Euler !

[Anonyme]

L'une des suite vient de la méthode de euler. L'autre ne figure pas dans la méthode de euler. D'ou vient-elle ?

Pour la preuve de l'existence avec les suite adjacente je verrai cela demain.

Avec tous les devoirs, recherches et projets qu'on nous donne ces temps ci je doute que je puisse voir la preuve avant les vacances.

[Anonyme]

Ici, les suites adjacentes stipulées par Benekire ne viennent pas de nulle part mais de la méthode d'Euler !

Je viens de voir la demo , je l'ai bien assimiler et je sais la refaire. Je veux bien que vienne de la méthode de Euler par contre je ne vois toujours pas d'où peut venir .

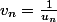
Je vous vois entrain de me dire que mais a partir de on peut former une infinité de suite alors pourquoi cette suite en particulier. Je n'imagine pas que Euler a eu un coup de chance ou bien qu'il s'est amuser a essayer beaucoup d'autre suites.

[Ben314]

Tu a vu dans la question 3)a) du T.P. que, si une telle fonction f existe, elle doit vérifier f(x)=1/f(-x).
Si tu as trouvé une suite de fonctions Un(x) telle que f(x)1/Un(-x).
Si tu part de Un(x)=(1+x/n)^n alors 1/Un(-x) vaut... (1-x/n)^(-n)

[Anonyme]

Tu a vu dans la question 3)a) du T.P. que, si une telle fonction f existe, elle doit vérifier f(x)=1/f(-x).
Si tu as trouvé une suite de fonctions Un(x) telle que f(x)1/Un(-x).
Si tu part de Un(x)=(1+x/n)^n alors 1/Un(-x) vaut... (1-x/n)^(-n)

Merci

Si j'ai bien compris :

est "encadrée" par et puisque si :

-
- alors

avec

Je trouve cela un peu léger pour justifier l'emploi de , je ne suis pas très convaincu portant je suis sur que quelque chose m'échappe..

[Anonyme]

Alors vous en pensez quoi ?