Exerice pas évident !

[Anonyme]

Salut , j'ai un exercice à faire trop dur !!!! y'a un graphe à tracer si quelqu'un pourrez me faire voir approximativement si il est possible de faire une courbe sur ce forum ?

RAPPEL :
Pour a > 0, a^x = e^x ln (a)

1. Tracer rapidement, dans un même système d’axes, le graphe des fonctions f (x) = x^4 et g(x) = 4^x.
2. En déduire que l’équation f(x) = g(x) a une seule racine < 0.
3. Trouver une racine évidente de l’équation f(x) = g(x).
4. Montrer que, pour x > 0, f(x) = g(x) <=> (ln(x) / x) = (ln (4) / 4).
5. Etudier le sens de variations de la fonction h(x) = (ln (x) / x).
Quelle est la valeur du maximum de la fonction h(x) ?
6. Donner les valeurs des racines > 0 de l’équation x^4 = 4^x.


Si vous pourriez me donner des pistes sérieuses ca serait vraiment cool..:) Je compte sur vous ..

[Chimerade]

2 ) On sait que est une fonction croissante sur R. Par contre est décroissante sur . La différence est donc croissante. Elle croît de 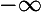à 1 quand x croît de 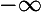à 0. En un seul point dans cet intervalle, la différence est nulle.

3) racine évidente 4

4)




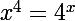
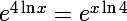
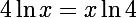
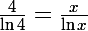
Je te laisse faire 5 et 6 qui sont tout aussi faciles que 1,2,3 et 4 !
A noter : la fonction ne passe pas par un maximum, mais par un minimum ! Erreur du professeur ? ou faute de recopie de ta part ?

[Romain18]

Pour la 4, si on te dit que x>0 ca te ramène a la formule ou tu transforme les puissance avec l'exponentiel et le logarithme ;)

[Anonyme]

Ben c'est bien ça sur le bouquin mais je crois que c'est lui qui a fais tous les exercices car c'est son propre bouquin donc peut etre une erreur de sa part mais ça m'etonnerait quand meme , tu es sur de ça ?

Par contre pour le graphe comment il faut faire ? je vois pas du tout..

Merci bien

[Nicolas_75]

Quel est ton problème précisément ?

[Anonyme]

Pour le graphe il faut juste prendre plusieurs valeurs de x et tracer la courbe c'est tout?

Désolé mais je comprends pas la question 5 ! lol

[Anonyme]

Ben y'a un maximum quand meme , lorsque la courbe est la plus haute quoi meme si c'est dans les nègatifs , enfin je pense que c'est ça , les autres vous croyez que y'a erreur dans la question ou vous pensez comme moi? ;)

[Chimerade]

Je te laisse faire 5 et 6 qui sont tout aussi faciles que 1,2,3 et 4 !
A noter : la fonction ne passe pas par un maximum, mais par un minimum ! Erreur du professeur ? ou faute de recopie de ta part ?

Je corrige : faute de lecture de ma part ! Mille excuses ! Au lieu d'étudier la fonction Ln(x)/x, j'avais étudié la fonction x/ln(x). Donc, effectivement, la fonction Ln(x)/x passe bien par un maximum et non pas par un minimum.

[Anonyme]

La dérivée h ' (x) il faut bien la calculer et faire un tableau de variations pour cela ?

Je trouve h' (x) = ( - 1/x) / x². C'est juste ?

[Anonyme]

Je pense que ma dérivée est fausse car je n'arrive pas a faire le tableau de variations , donc que trouvez vous et quels sont les solutions ?

Merciiii

[Anonyme]

Personne ???? SNifff c'est pour demain cest assez pressant !!

De plus j'adore quand à la fin , je me couche , et j'ai tout compris !!

Jattends vos aides...

[Anonyme]

Le 5 est fait , je trouve e comme valeur pour laquelle h ' ( x) s'annule est ce cela? Pourquoi je narrive pas a calculer ln (e) /e sur ma machine ?

[Anonyme]

Dernière question :
Tu as vu que le max (unique extremum) de la fn ln(x)/x est le point (e,1/e), soit un point au dessus de l'axe des x. Comme la fn repart vers -inf quand x va vers + inf, et que ln4/4 est inférieur à 1/e, il y a seulement 2 solutions à l'équation ln(x)/x = ln4/4.
Or ln4/4 = ln2²/4=2ln2/4=ln2/2
On a donc 2 solutions évidentes : 4 et 2. Ce sont les seules.

A+

Le tamanoir

[Nicolas_75]

Bonjour,

Si h(x) = ln(x) / x
Alors h'(x) = [(1/x).x-ln(x)] / x^2 = [1-ln(x)] / x^2
non ?

Nicolas

[Anonyme]

Ben, de 0 à e ca croit , et de e à + linfini ca décroit, et le maximum est donc 1/e , c'est ce que je trouve pour la 5. ( La dérivée j'avais trouvé ! ;))
Tamanoir ,tu as donc répondu à la 6 ?

merci de me rép..

[Anonyme]

Oui, je parlais de la 6. On est d'accord.