Bonjour,
J’ai un exercice dont j’ai la réponse mais pas le résonnement. au moins je ne peux pas maintenant ce que je dois utiliser pour trouver la solution :
https://image.ibb.co/bubjOn/ds.jpg
cordialement .
Exercise sur develepment des limits
8 messages
- Page 1 sur 1
exercise sur develepment des limits
Modifié en dernier par josephdzrob01 le 09 Mai 2018, 14:19, modifié 1 fois.
Re: exercise sur develepment des limits
josephdzrob01 a écrit:Bonjour,
J’ai un exercice dont j’ai la réponse mais pas le résonnement. au moins je ne peux pas maintenant ce que je dois
Bonjour Je ne comprends pas bien ta question. Que veux-tu au juste?
P.S Les cloches résonnent pendant que les mathématiciens raisonnent.
Re: exercise sur develepment des limits
merci pour comment
mon question , si comment on va faire cette exo et merci
mon question , si comment on va faire cette exo et merci
Re: exercise sur develepment des limits
Salut,
Tu fixe un réel et, pour tout
et, pour tout  tu pose
tu pose \!=\!f(a\!+\!y)f(a\!-\!y)) .
.
Par hypothèse, tu as donc\!\leq\! g(0)) pour tout
pour tout  .
.
Ensuite, étudie la fonction : c'est quoi
: c'est quoi ) ?
? ) ? et
? et ) ?
? ) ?
?
Si on avait\!>\!0) , qu'est ce que ça signifierais concernant les variations de
, qu'est ce que ça signifierais concernant les variations de  (au alentour de 0) ?
(au alentour de 0) ?
le signe de ? Qu'en déduirait on concernant
? Qu'en déduirait on concernant  ?
?
Tu fixe un réel
Par hypothèse, tu as donc
Ensuite, étudie la fonction
Si on avait
le signe de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: exercise sur develepment des limits
merci pour l'aide, mais j'ai une petite question comment nous obtenons: g(y)<=g(0)
Re: exercise sur develepment des limits
Ben314 a écrit:Salut,
Tu fixe un réelet, pour tout
tu pose
.
Par hypothèse, tu as doncpour tout
.
Ensuite, étudie la fonction: c'est quoi
?
? et
?
?
Si on avait, qu'est ce que ça signifierais concernant les variations de
(au alentour de 0) ?
le signe de? Qu'en déduirait on concernant
?
Merci pour L'aide Dr , J'ai obtenu le chemin que vous suguest tome, mais j'ai toujours un petit problème à porve que g '' (0)> 0, alors s'il vous plaît aidez-moi de vous.
Re: exercise sur develepment des limits
Si on fixe  et que, pour tout
et que, pour tout  on pose
on pose \!=\!f(a\!+\!y)f(a\!-\!y)) alors :
alors :
(1)\!=\!\big(f(a)\big)^2) donc l'hypothèse de l'énoncé nous dit que
donc l'hypothèse de l'énoncé nous dit que \!\leq\!g(0)) pour tout
pour tout 
(2) La fonction est de la forme
est de la forme  de dérivée
de dérivée 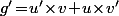 , c'est à dire :
, c'est à dire :
=f'(a\!+\!y)f(a\!-\!y)-f(a\!+\!y)f'(a\!-\!y)\ \ \text{ pour tout }\ y\!\in\!{\mathbb R})
(car la dérivé de) est
est ) )
)
\!=\!f'(a)f(a)\!-\!f(a)f'(a)\!=\!0)
(2) On calcule de même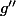 :
:
=\Big[f''(a\!+\!y)f(a\!-\!y)-f'(a\!+\!y)f'(a\!-\!y)\Big]-\Big[f'(a\!+\!y)f'(a\!-\!y)-f(a\!+\!y)f''(a\!-\!y)\Big])
f(a\!-\!y)\!-\!2f'(a\!+\!y)f'(a\!-\!y)\!+\!f(a\!+\!y)f''(a\!-\!y)\ \ \text{ pour tout }\ y\!\in\!{\mathbb R})
\!=\!f''(a)f(a)\!-\!2f'(a)f'(a)\!+\!f(a)f''(a)\!=\!2\Big[f''(a)f(a)\!-\!\big(f'(a)\big)^{\!2}\Big])
(3) Si on avait\!>\!0) alors, vu que
alors, vu que 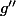 est supposée continue, elle serait >0 sur un certain intervalle
est supposée continue, elle serait >0 sur un certain intervalle  avec
avec 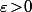 ce qui signifierais que
ce qui signifierais que  est strictement croissante sur
est strictement croissante sur  .
.
Or, comme\!=\!0) , cela impliquerais que
, cela impliquerais que  sur
sur  donc que
donc que  est strictement croissante sur
est strictement croissante sur  .
.
Sauf que c'est en contradiction avec le fait que\!\leq\!g(0)) pour tout
pour tout  .
.
(4) on a donc forcément\!\leq\!0) , c'est à dire
, c'est à dire f(a)\!\leq\!\big(f'(a)\big)^{\!2})
(1)
(2) La fonction
(car la dérivé de
(2) On calcule de même
(3) Si on avait
Or, comme
Sauf que c'est en contradiction avec le fait que
(4) on a donc forcément
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: exercise sur develepment des limits
Ben314 a écrit:Si on fixeet que, pour tout
on pose
alors :
(1)donc l'hypothèse de l'énoncé nous dit que
pour tout
...........
(4) on a donc forcément, c'est à dire
merci beaucoup monsieur, vous m'avez vraiment aidé j'essayais de le résoudre avec une autre chose qui ne m'aidera jamais.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
