Exercices sur les suites ! =)
56 messages
- Page 3 sur 3 - 1, 2, 3
Non je suis pas mathématicien et de deux vous avez vus vos réponses !!!
On ne comprenait plus rien, je suis partis sur du copié coller mais rien n'était juste même l'énoncé !! on peut y lire Un pour Vn ...
Je retombais pas sur mes pieds, en plus avec mes fichus problème de LaTeX ...
Tu aurais pu avoir l'amabilité de tout lui clarifier. Tu n'y devais pas y avoir très clair non plus. Moi je l'avoue.
En tout cas si il y a encore besoin d'aide je serais là :)
L'erreur est humaine, c'est pour ça que le brouillon existe et que l'on "met" au propre à la fin. Et non pas commencer le propre comme un brouillon.
On ne comprenait plus rien, je suis partis sur du copié coller mais rien n'était juste même l'énoncé !! on peut y lire Un pour Vn ...
Je retombais pas sur mes pieds, en plus avec mes fichus problème de LaTeX ...
Tu aurais pu avoir l'amabilité de tout lui clarifier. Tu n'y devais pas y avoir très clair non plus. Moi je l'avoue.
En tout cas si il y a encore besoin d'aide je serais là :)
L'erreur est humaine, c'est pour ça que le brouillon existe et que l'on "met" au propre à la fin. Et non pas commencer le propre comme un brouillon.
Et bien je t'affirme que si, j'y vois très clair.
Mais le but n'est pas de montrer a l'élève qu'on y voit très clair mais de l'aider lui a y voir clair. Je donne donc des indices que je vais ensuite rédiger d'une manière différente s'ils sont incompris. Donc oui ca ressemble à un brouillon forcement, c'est morceau par morceau car j'estime inutile de pondre une solution à l'élève sans lui donner l'occasion de chercher.
L'erreur est humaine oui, j'en fais d'ailleur tout les jours, mon post n'est pas tourné contre ton erreur mais contre ton agressivité lorsque tu écris "relis toi !!!!!!!!!" alors que c'est toi qui te trompais et j'en passe ... Si c'est pour s'énerver, ne post pas.
Mais le but n'est pas de montrer a l'élève qu'on y voit très clair mais de l'aider lui a y voir clair. Je donne donc des indices que je vais ensuite rédiger d'une manière différente s'ils sont incompris. Donc oui ca ressemble à un brouillon forcement, c'est morceau par morceau car j'estime inutile de pondre une solution à l'élève sans lui donner l'occasion de chercher.
L'erreur est humaine oui, j'en fais d'ailleur tout les jours, mon post n'est pas tourné contre ton erreur mais contre ton agressivité lorsque tu écris "relis toi !!!!!!!!!" alors que c'est toi qui te trompais et j'en passe ... Si c'est pour s'énerver, ne post pas.
melik tu sors ! :mur:
Mais pour finir même moi, j'étais perdu dans vos posts alors M2a j'espère qu'elle a suivie le fil directeur de la discussion et qu'elle sera finir et comprendre son exercice.
Il faut pas hésiter à lui dire qu'elle c'est tromper dans son énoncé ... et dans les calculs des premiers termes. Car elle tournait en rond la pauvre. :--:
PS: Arnaud je vois que tu connais le LaTeX, ce langage est magnifique et permet une mise en forme extraordinaire qui favorise la clarté d'un topic comme celui-ci. Alors n'hésites pas à t'en servir :++:
Mais pour finir même moi, j'étais perdu dans vos posts alors M2a j'espère qu'elle a suivie le fil directeur de la discussion et qu'elle sera finir et comprendre son exercice.
Il faut pas hésiter à lui dire qu'elle c'est tromper dans son énoncé ... et dans les calculs des premiers termes. Car elle tournait en rond la pauvre. :--:
PS: Arnaud je vois que tu connais le LaTeX, ce langage est magnifique et permet une mise en forme extraordinaire qui favorise la clarté d'un topic comme celui-ci. Alors n'hésites pas à t'en servir :++:
Merci à tous pour vos réponses ! =D
Excusez moi si les questions étaient faites un peu dans le désordre !
En tout cas vous m'avez tous les deux permis de répondre à la majorité des questions !
Il ne m'en reste que deux !
J'avais trouvé que la suite Vn était une suite arithmétique de raison r=3 mais d'une autre façon !
Seulement je pense savoir me débrouiller pour les deux dernières questions, mais est ce que vous auriez l'amabilité de m'expliquer comment exprimer Vn en fonction de n à partir de Vn+1= Vn+3, pour le reste je pense que je saurais me débrouiller !
Merci encore pour votre aide .
Excusez moi si les questions étaient faites un peu dans le désordre !
En tout cas vous m'avez tous les deux permis de répondre à la majorité des questions !
Il ne m'en reste que deux !
J'avais trouvé que la suite Vn était une suite arithmétique de raison r=3 mais d'une autre façon !
Seulement je pense savoir me débrouiller pour les deux dernières questions, mais est ce que vous auriez l'amabilité de m'expliquer comment exprimer Vn en fonction de n à partir de Vn+1= Vn+3, pour le reste je pense que je saurais me débrouiller !
Merci encore pour votre aide .
Hello,
Une suite arithmétique, c'est une suite où pour passer d'un terme au suivant, on ajoute r.
Partons de ,
,
j'ajoute r, j'arrive à (
(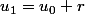 )
)
j'ajoute encore r j'arrive à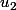 (
( )
)
j'ajoute encore r j'arrive à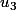 (
( )
)
etc ...
Donc pour aller jusque il faut ajouter n fois r à
il faut ajouter n fois r à  .
.
Et .
.
Je t'ai envoyé un lien hier en message privé qui explique rapidement tout ça.
Si ca peut t'aider voici une illustration que je propose souvent à mes élèves pour bien visualiser les choses :
Il faut considérer qu'une suite arithmétique c'est comme une échelle dont les barreaux sont espacés d'une distance r.
Ainsi tu visualises combien de fois il faut parcourir la distance r pour passer d'un barreau à l'autre.
On voit donc que mais si la suite ne démarre pas à
mais si la suite ne démarre pas à  mais à
mais à  , il faudra parcourir une fois en moins la distance r (puisque l'on part un barreau plus haut).
, il faudra parcourir une fois en moins la distance r (puisque l'on part un barreau plus haut).
Donc.r) etc ...
etc ...

Une suite arithmétique, c'est une suite où pour passer d'un terme au suivant, on ajoute r.
Partons de
j'ajoute r, j'arrive à
j'ajoute encore r j'arrive à
j'ajoute encore r j'arrive à
etc ...
Donc pour aller jusque
Et
Je t'ai envoyé un lien hier en message privé qui explique rapidement tout ça.
Si ca peut t'aider voici une illustration que je propose souvent à mes élèves pour bien visualiser les choses :
Il faut considérer qu'une suite arithmétique c'est comme une échelle dont les barreaux sont espacés d'une distance r.
Ainsi tu visualises combien de fois il faut parcourir la distance r pour passer d'un barreau à l'autre.
On voit donc que
Donc

Il faut juste revenir à la manière dont on a construit  :
:
 Cette expression nous donne
Cette expression nous donne  en fonction de
en fonction de  , il faut la modifier pour avoir
, il faut la modifier pour avoir  en fonction de
en fonction de  .
.
Et la on remplace par l'expression que l'on a trouver et ca nous donne
par l'expression que l'on a trouver et ca nous donne  en fonction de n, et la ca saute aux yeux que la suite converge vers zéro : on peut démontré que ce que l'on a conjecturé est donc vrai.
en fonction de n, et la ca saute aux yeux que la suite converge vers zéro : on peut démontré que ce que l'on a conjecturé est donc vrai.
Et la on remplace
Ce qu'évoque Teacher ici permet de trouver la limite -eventuelle- d'une suite.
Lorsque l'on a trouvé l qui vérifie l = f(l) alors on peut dire que si la suite converge, alors elle converge vers l.
Seulement on a pas montré qu'elle convergeait, on l'a juste conjecturé.
L'exercice t'amène jusqu'à trouver l'expression de en fonction de n. Et cette expression permet de conclure tout de suite à la convergence de
en fonction de n. Et cette expression permet de conclure tout de suite à la convergence de  vers 0, comme je l'ai dis dans mon précédent post.
vers 0, comme je l'ai dis dans mon précédent post.
Il ne sert donc ici à rien de cherche l tel que l = f(l).
Lorsque l'on a trouvé l qui vérifie l = f(l) alors on peut dire que si la suite converge, alors elle converge vers l.
Seulement on a pas montré qu'elle convergeait, on l'a juste conjecturé.
L'exercice t'amène jusqu'à trouver l'expression de
Il ne sert donc ici à rien de cherche l tel que l = f(l).
Arnaud-29-31 a écrit:Il faut juste revenir à la manière dont on a construit:
Cette expression nous donne
en fonction de
, il faut la modifier pour avoir
en fonction de
.
Et la on remplacepar l'expression que l'on a trouver et ca nous donne
en fonction de n, et la ca saute aux yeux que la suite converge vers zéro : on peut démontré que ce que l'on a conjecturé est donc vrai.
[FONT=Arial][FONT=Microsoft Sans Serif][FONT=Microsoft Sans Serif]Bonjour,
J'ai également à faire cet exercice en devoirs, et vos conseils m'ont beaucoup aider,
Cependant je ne comprends toujours pas comment exprimer Un en fonction de n ,
Pourriez-vous m'aider s'il-vous-plaît .
Merci d'avance [/FONT] [/FONT] [/FONT]
Bonjours à tous, je suis en seconde et dans un exercice on me demande:
Dans un repère orthonormé du plan, tracer le cercle de centre E(3;2) passant par A(5;-1)
1- Calculer le rayon du cercle (déjà fait)
2-On considère un point M(0;y) Montrer que EM(au carré)=y(au carré)-4y+13.
3-En déduire les points d'intersection du cercle avec l'axe des ordonnées.
J'avoue que je bloque un peu pour la 2 et la 3 :hum: AIDERRRRRR MOIIIIIIII §§ :triste: :cry:
Merci d'avance ! :lol4:
Dans un repère orthonormé du plan, tracer le cercle de centre E(3;2) passant par A(5;-1)
1- Calculer le rayon du cercle (déjà fait)
2-On considère un point M(0;y) Montrer que EM(au carré)=y(au carré)-4y+13.
3-En déduire les points d'intersection du cercle avec l'axe des ordonnées.
J'avoue que je bloque un peu pour la 2 et la 3 :hum: AIDERRRRRR MOIIIIIIII §§ :triste: :cry:
Merci d'avance ! :lol4:
56 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
