Exercices sur les produits scalaires

[giogiodu59282]

Bonjour à toi aussi !!

on a les points M(1;3) N(4;1) et P(3;6)
demontrer que les droites (MP) et (MN) sont perpendiculaires ?
quel est l'ensemble des points S tels que vecteur MS . vecteur MP = 0 ?
je n'arrive pas à résoudre cet exercice pourriez vous m'expliquer merci

[Ericovitchi]

Et bien si tu essayais de démontrer que les vecteurs MP et MN sont perpendiculaires en calculant leur produit scalaire par exemple ?

[Frednight]

Petit rappel de cours : lorsque deux vecteurs (x,y) et (x',y') sont perpendiculaires, alors = 0

d'autre part, = xx'+yy'

A toi de mettre en équation

[Timothé Lefebvre]

Petit rappel de cours : lorsque deux vecteurs (x,y) et (x',y') sont perpendiculaires, alors = 0

Salut,

deux vecteurs ne sont pas perpendiculaires !!

On dira que deux vecteurs sont orthogonaux si leur produit scalaire est nul.

De même, (x,y) et (x',y') ont des directions orthogonales si, et seulement si, xx' + yy' = 0

[Frednight]

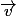
désolé pour cette erreur et merci de m'avoir corrigé. Une question : peut-on aussi dire que deux vecteurs sont "normaux" ou est-ce que cette expression est réservée à des énoncés tels que "soit vecteur normal à la droite (d)"?

[Timothé Lefebvre]

Non, on pourra juste parle de vecteur normal à une droite du plan, ou normal à une surface.

[Frednight]

d'accord

merci pour cette réponse