Bonjour à tous !
Voici quelques exos de révisions pour ceux qui viennent de passer le bac

Ne vous fiez pas à la difficulté des premiers exercices, la difficulté est croissante.
I) Résoudre les équations suivantes dans

:
 \qquad (1-i)z^2 - 2(3-2i)z + 9 - 7i = 0)
 a) \quad z^2 - (3-2i)z + 8 + 6i = 0)
 b) \quad z^4 - (3-2i)z^2 + 8 + 6i = 0) II)
II) Soit l'équation
z-20 = 0)
, z
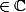
1)

Déterminer le réel a tel que
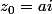
soit une des racines de cette équation. Déterminer alors les deux autres racines
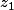
et
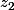
.
2)

Le plan P est rapporté à un repère orthonormal
)
. On appelle A,B,C les points d'affixes respectives
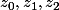
. Déterminer l'affixe du barycentre des points A,B,C affectés respectivement des coefficients -1,1,1. Déterminer l'ensemble des points M de P tels que :
-MA² + MB² + MC² = 36
III) 1)

Résoudre l'équation :
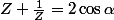
,
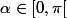
Ecrire les solutions sous forme d'une exponentielle complexe en fonction de

2)

En déduire les solutions de l'équation :
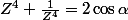
,
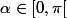 IV)
IV) Le plan est rapporté à un repère orthonormal
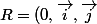)
. On considère le point A(2,3) et la droite D d'équation
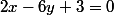
1)

Calculer la distance de A à D.
2)

Déterminer les coordonnées du projeté orthogonal H de A sur D, retrouver la distance de A à D.
V) Soit (E) l'équation différentielle :
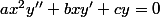
,
 \in \mathbb{R}^*\times\mathbb{R}^2)
1) En posant
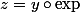
c'est à dire
=y(e^t))
, ce qui revient à faire le changement de variable
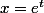
, montrer que y est solution de (E) sur
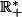
si et seulement si z est solution d'une équation du second ordre à coefficients constants que l'on précisera. Comment procéder pour obtenir une équation du second ordre à coefficients constants équivalent à (E) sur
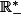
?
2)

Résoudre l'équation différentielle :
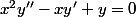
.
3)

Déterminer toutes les applications f deux fois dérivables sur
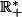
telles que :
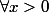
,
=f(\frac{1}{x}))
, laissez tomber la question 2) et} \\ \textit{pour la question 3), etablissez l'equation differentielle sans la resoudre.}) VI)
VI) Dans cet exercice
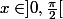
est un réel fixé.
1)

On considère la suite
)
définie par :
 \mathrm{ , } \forall n \in \mathbb{N}\\<br /> \end{array}<br /> \right.)
a) Montrer que la suite de terme général
)
est géométrique.
b) En déduire que pour tout entier n l'expression de

en fonction de x et de n.
Montrer que la suite
)
est convergente est donner sa limite.
On définit les deux suite
)
et

par :
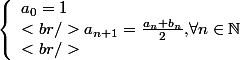
et
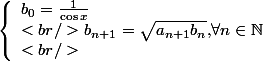
2) a) Exprimer

comme quotient de deux cosinus.
b) Montrer que
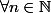
,
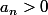
et
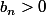
.
3) a) Montrer que :
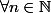
,
}(b_n-a_n))
b) Montrer que
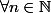
,
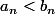
.
c) En déduire que
)
est croissante et
)
décroissante.
d) Montrer que :
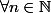
,
)
e) Montrer que les suite
)
et
)
sont convergentes et ont la même limite notée L.
4) a) Montrer que :
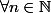
,
}{\cos ^2 x})
,
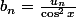
b) En déduire la valeur de L.
VII) (Exercice de spé) Soit p un nombre premier.
a) Soit k un entier tel que
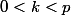
.
Montrer que
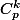
est divisible par p.
b) Soient a et b dans

, montrer que :
^p-a^p-b^p)
.
c) En déduire que :
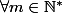
,
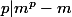
d) Montrer que si m et p sont premiers entre eux alors :