Voilà ce que j'ai fait
II :
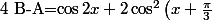+2\cos^2 \left(x+\frac{2\pi}{3}\right))
, mais là je ne vois pas trop comment réduire ça.

Ensuite, pour trouver
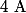
et
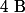
, connaissant

et

, on trouve
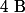
et on en déduis
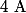
, mais comme je suis pas sûr de

, je n'ai rien fait.
III : Je trouve comme couple solution :
; \(1;\frac{1}{2}\) \})
.
Si on prends le premier couple :
- et si

et

pris dans cet ordre, forment trois termes consécutifs d'une suite arithmétrique alors la raison est

- et si

et

pris dans cet ordre, forment trois termes consécutifs d'une suite géométrique alors la raison est

Si on prends le second couple :
- et si

et

pris dans cet ordre, forment trois termes consécutifs d'une suite arithmétrique alors la raison est

- et si

et

pris dans cet ordre, forment trois termes consécutifs d'une suite géométrique alors la raison est

Et voilà le travail :ptdr:
