Exercices corrigés mais incompris sur trinôme

[darkomen]

Bonsoir a tous,

Je fait appel a vous car je me refait des exercices que j'ai fait il y a deja quelques mois mais je bloque sur un en particulier auquel je n'arrive pas trop a comprendre la démarche pour le résoudre.

En voici le détails:






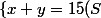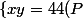x et y sont racines de X² - Sx + P = 0



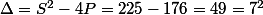
Ce qui donne 2 racines de valeurs 11 et 4.

---------------------------------------------------------------------------------

Je suis bien d'accord que x + y est bien une somme de racines S et
xy un produit de racines P mais en quoi peut-on déduire l'équation ?
X² - Sx + P = 0
et ainsi en quoi peut-on aussi déduire le descriminant de la sorte ?



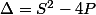
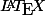
PS:optionnellement comment faites vous pour écrire en un système avec une grande accolade et plusieurs lignes lui correspondant ?


Merci a vous de votre aide 8)

[math*]

Si x et y sont deux racines de ax²+bx+c alors :

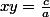
et

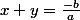
[darkomen]

Si x et y sont deux racines de ax²+bx+c alors :

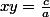
et

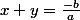
Cela ne m'avance pas beaucoup mais alors dans ce cas peut-on dire que
l'expression X²-Sx+P=0 est toujours vrai ?

[math*]

Ah ben moi je crois que ça t'avance beaucoup.
On te dit : x+y=S
et xy=P
et xy=c/a, si a =1, c=P

Pareil avec x+y=S
x+y=-b/a
avec a=1, x+y=-b
donc b=-S, ce qui est bien le cas dans x²-Sx+P=0

[math*]

x²-Sx+P=0 est toujours vraie si a=1 dans ax²+bx+c.

[anima]

PS:optionnellement comment faites vous pour écrire en un système avec une grande accolade et plusieurs lignes lui correspondant ?

\{eq1\\eq2\\eq3\\...\\eqn :zen:

[Flodelarab]

ah ouai ça donne ça:


Ya des jours ou on n'a pas envie de faire des posts constructifs :ptdr:

[darkomen]

Ah ben moi je crois que ça t'avance beaucoup.
On te dit : x+y=S
et xy=P
et xy=c/a, si a =1, c=P

Pareil avec x+y=S
x+y=-b/a
avec a=1, x+y=-b
donc b=-S, ce qui est bien le cas dans x²-Sx+P=0

Ok merci Maths j'ai compris la logique.Par contre dans ce cas on a de la chance de constater que si a=1 il resoud bien le système mais si on ne peux pas supprimer le dénominateur comme on a fait ca deviens beaucoup plus complexe.

Mais j'ai effectue compris le truc.Ca montre bien que tu as la gym des maths la ou moi je ne pensais pas a la technique de la supposition :zen:

Bien joué et merci a toi