le plan complexe est rapporté à un repère orthonormal direct(O;u,v) on désigne par A le point d'affixe i. A tout point M du plan, distinct de A d'affixe z, on associe le point M' d'affixe z' définie par:
z'=(z^2)/(i-z)
1.déterminer les points M confondus avec leur image M'.
2.on pose z=x+iy et z'=x'+iy' avec x,y,x' et y' réels
a.démontrer que x'=(-x(x^2+y^2-2y)) / (x^2+ (1-y)^2)
b. deduisez en l'ensemble E des points M dont l'image M' est située sur l'axe des imaginaires purs
Bon bbaa voila j'ai un exercice a maths(et les maths c'est pas mon fort!!! :triste: ) a faire mais je n'y arrive je ne sais faire aucune de ces questions et pourtant j'ai cherché :mur: alors je me demandais si vous pouviez m'aider parce que je ne comprends rien de rien
merci d'avance
Exercice trop compliqué sur les complexes
3 messages
- Page 1 sur 1
salut, bonjour s'il vous plait...
il faut resoudre z=z'
il suffit que tu remplaces z par x+iy ds z²/(i-z) et ensuite tu identifies partie réelle et imaginaire avec z'=x'+iy'
on a :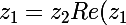=Re(z_2)) et
et =Im(z_2))
bon courage
plan complexe est rapporté à un repère orthonormal direct(O;u,v) on désigne par A le point d'affixe i. A tout point M du plan, distinct de A d'affixe z, on associe le point M' d'affixe z' définie par:
z'=(z^2)/(i-z)
1.déterminer les points M confondus avec leur image M'.
il faut resoudre z=z'
2.on pose z=x+iy et z'=x'+iy' avec x,y,x' et y' réels
a.démontrer que x'=(-x(x^2+y^2-2y)) / (x^2+ (1-y)^2)
b. deduisez en l'ensemble E des points M dont l'image M' est située sur l'axe des imaginaires purs
il suffit que tu remplaces z par x+iy ds z²/(i-z) et ensuite tu identifies partie réelle et imaginaire avec z'=x'+iy'
on a :
bon courage
BILIMOUN1234 a écrit:le plan complexe est rapporté à un repère orthonormal direct(O;u,v) on désigne par A le point d'affixe i. A tout point M du plan, distinct de A d'affixe z, on associe le point M' d'affixe z' définie par:
z'=(z^2)/(i-z)
1.déterminer les points M confondus avec leur image M'.
2.on pose z=x+iy et z'=x'+iy' avec x,y,x' et y' réels
a.démontrer que x'=(-x(x^2+y^2-2y)) / (x^2+ (1-y)^2)
b. deduisez en l'ensemble E des points M dont l'image M' est située sur l'axe des imaginaires purs
Bon bbaa voila j'ai un exercice a maths(et les maths c'est pas mon fort!!! :triste: ) a faire mais je n'y arrive je ne sais faire aucune de ces questions et pourtant j'ai cherché :mur: alors je me demandais si vous pouviez m'aider parce que je ne comprends rien de rien
merci d'avance
Salut
1/
Comme on te l'a suggéré pose

donc
 tu factorises et en déduis les valeurs de z solutions
tu factorises et en déduis les valeurs de z solutions2/
Commence par simplifier l'expression
 après tu remplaces
après tu remplaces  par
par  et
et  par
par  et tu identifies.La réponse au b viendra d'elle même
et tu identifies.La réponse au b viendra d'elle même
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
