Exercice Trigonométrie 1ere sti2d

[Ginklaw]

Bonjour, je bloque sur un exercice de math, pouvez-vous m'aider.

L'exercice en question:http://imgur.com/5WgMUyw
Pour l'exercice 1 voila ce que je trouve:

- a) [0;1]
b)AP=AC-x
2)a)AH=(1-x)*cos(60)

Je bloque sur le reste.

Merci.

[mathelot]

Cours



Pythagore

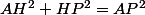
[Ginklaw]

Bonjour, désoler pour le temps de réponse mais je ne comprend pas très bien ce que tu veux me dire.

[mathelot]

Bonjour, désoler pour le temps de réponse mais je ne comprend pas très bien ce que tu veux me dire.

que les éléments de cours nécessaires à la résolution de l'exercice sont les valeurs remarquables du cosinus et le théorème de Pythagore.

[Shew]

Cours



Pythagore

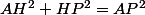
Ou pour simplifier la démarche :lol3:

[Ginklaw]

Je ne comprend pas comment trouver une valeur sachant que je trouve :Cos(60)=AM/AP
=AM/1-x.

[Shew]

Je ne comprend pas comment trouver une valeur sachant que je trouve :Cos(60)=AM/AP
=AM/1-x.

remplacez par les valeurs appropriées .

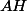
Et c'est pas

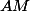
[Ginklaw]

ça donne : 1-x*1/2=AM puis 1-x=AM/1/2 ce qui me dérange c'est le x.

[Shew]

ça donne : 1-x*1/2=AM ce qui me dérange c'est le x.

Le x est légitime puisque le point M est mobile sur

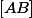
[Ginklaw]

Ok, mais pour que AMP soit rectangle en M dans la question b il faut que x = AH ?

[Shew]

Ok, mais pour que AMP soit rectangle en M dans la question b il faut que x = AH ?

Donc AM = AH c'est à dire que M et H sont confondus .

[Ginklaw]

Oui le problème c'est que la question demande une valeur et que même en utilisant cos je ne vois pas comment la donner.

[Shew]

Oui le problème c'est que la question demande une valeur et que même en utilisant cos je ne vois pas comment la donner.

On connait AM et on a déduit AH de plus on a AM = AH on a donc :

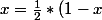[Ginklaw]

Ok, je trouve la même expression donc la valeur de x pour que AMP sit rectangle en M est 1/2*(1-x) ?

[Shew]

Ok, je trouve la même expression donc la valeur de x pour que AMP sit rectangle en M est 1/2*(1-x) ?

Non on résout l’équation que je vous donne plus haut c'est à dire

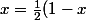[Ginklaw]

Cela donne 1/3=x donc x a pour valeur :1/3 ?

[Shew]

Cela donne 1/3=x donc x a pour valeur :1/3 ?

C'est correct

[Ginklaw]

Ok, j'ai également trouver la 3. PH=(1-x)*racine3/2, maintenant pour la 4.a je ne sait pas comment avoir la hauteur.

[Shew]

Ok, j'ai également trouver la 3. PH=(1-x)*racine3/2, maintenant pour la 4.a je ne sait pas comment avoir la hauteur.

Comme avec HP ou en utilisant le théorème de Pythagore en vous rappelant des règles sur les droites remarquables dans un triangle équilatéral .

[Ginklaw]

donc sin(60)=CD/AC (D est le point au milieu du segment AB)
1* racine3/2=CD
racine3/2=CD ?