Exercice

[Niki]

Salut j'ai un petit souci avec un Exercice ces un peut trop long à écrire. La partie qui me pose est la svt : (E)=2z^2+3zbarr^2=5+i
La question est la suivante déterminer l'ensemble des nombre complexe vérifiant la relation (E) .
Merci davantage.

[sofianmakhlouf]

Bonsoir
Tu peux poser z=x+iy

[vladi]

Bonjour



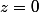n'est pas solution

on peut donc noter avec tout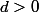

de plus on sait que (puisque z n'est pas nul)



ton ensemble E avec tout d>0 et les trois racines de

[vladi]

NB

la svt : (E)=2z^2+3zbarr^2=5+i

ma réponse précédente ok mais sous réserve que j'ai bien traduit l'écriture de E

3zbarr^2 moi je suppose qu'il s'agit de

mais là j'ai un doute avec le double "r" de "barr"

ça se trouve il fallait lire

[Sa Majesté]

ton ensemble E avec tout d>0 et les trois racines de

J'ai plus que des doutes, d dépendant de z

[vladi]

ton ensemble E avec tout d>0 et les trois racines de

J'ai plus que des doutes, d dépendant de z

hé oui d dépend de z !!

(je me suis arrêté là à l'écriture de ce polynôme du troisième degré mais certes il aurait été bien que je le dise à la fin)

je vais voir si je peux prendre du temps pour continuer

[vladi]

NB++
c'est vrai SaMajesté que en plus ça complique mon truc poly à trois degré

il y a la piste de Soufian Makhlouf qui me semble plus pertinente et que je viens de voir(il postait pendant que je faisait mon message)

[vladi]

erreur écriture du prénom
mes excuses "Sofian" (on ne peut pas éditer )

[Niki]

Bonsoir ; Vladi la réponse que vous avez posté à 20:56 j'aurais besoin d' un peut plus d'explication et de savoir comment résoudre une équation dont les inconnus sont pas les mêmes c'est-à-dire z et d .
Par rapport la question que vous vous demande ces 3zbar^2. Merci

[vladi]

Bonsoir ; Vladi la réponse que vous avez posté à 20:56 j'aurais besoin d' un peut plus d'explication et de savoir comment résoudre une équation dont les inconnus sont pas les mêmes c'est-à-dire z et d .
Par rapport la question que vous vous demande ces 3zbar^2. Merci

Bonsoir

il faut oublier ma réponse que j'ai écris pendant que Sofian Makhlouf postait sa réponse

la sienne est très pertinente et simple (la mienne complique tout d dépend de z et mon poly est de degré trois bref : il faut oublier et exploiter la réponse de l'autre intervenant )

désolé mais quand j'ai validé mon post je ne savais pas que quelqu'un d'autre avait fait un truc vraiment meilleur

[Niki]

Si je remplace z par x+iy et z bar par x-iy je veux avoir : 5x^2-y^2-2ixy=5+i
Par identification:
5x^2-y^2=5 <==> x^2-y^2=1
-2ixy=i <==>xy=1/2
maintenant je dois trouver les solutions qui vérifient la relation j'ai besoin d'idée.

[fatal_error]

slt,

ton recopiage ou tes calculs sont faux:
on doit trouver
5x^2-5y^2=5 <==> x^2-y^2=1
-2ixy=i <==>xy=- 1/2
ben apres tu prends x = -1/(2y)
et t'injectes dans x^2-y^2=1 et tu souffres un peu

[Niki]

Je veux faire ce que vous m'avez dit et je vous envoie la solution.

[Niki]

Bon j'ai eu comme solution:
Si x=1/2
Je le remplace dans x^2-y^2=1
alors je vais avoir (-1/2y)^2-y^2=1
1/4y^2-y^2=1 <==> (1-4y^4)/4y^2=1
1-4y^4=4y^2 <==>1-4y^4-4y^2=0
y^2 (-4y^2-4)-1=0 <==> -4y^2-4-1=0
-4y^2=5 <==> y =√(5/4) ou -√(5/4).

Merci.

[fatal_error]

t'as truffé des fautes de partout
deuxieme ligne, t'écris x=1/2...
tes divisions sont mal écrites: 1/(2y) et non 1/2y == y/2
au milieu, je lis pas vu que déjà la première ligne (1/4y^2-y^2=1) est fausse
et (des fois que t'aurais juste mal recopié) quand je lis la fin:
si t'injectes tes solutions dans l'eq du départ, je doute que tu satisfasse l'équation 2z^2+3zbarr^2=5+i

[Niki]

Sil vous plaît aide moi à le résoudre sa fait une semaine que je cherche à le corrigé

[fatal_error]

de (1):
posons


réel donc

on déduit
vérif par valeur numérique:

Code: Tout sélectionner

    octave:4> b=(sqrt(-2+2*sqrt(2)))/2; a=-1/(2*b);
    octave:5> 2*(a+i*b)^2+3*(a-i*b)^2-5-i
    ans =   -1.7764e-15
    octave:6> b=(-sqrt(-2+2*sqrt(2)))/2; a=-1/(2*b);
    octave:7> 2*(a+i*b)^2+3*(a-i*b)^2-5-i
    ans =   -1.7764e-15