Bonjour je suis en 1 ère S,
lors d'un exercice on nous demande de donner les valeurs de f(x)=0 pour la fonction f(x)= 4*x^3-12*x-1 (à 0,1 près)
on a vu lors de l'étude des variations de cette fonction que 3 valeurs étaient solution de f(x) = 0 le problème c'est que je ne voit pas comment les trouver, surement avec une résolution d'équation cubique mais je ne sait pas comment faire donc pourriez vous m'éclaircir sur le sujet s'il vous plait?
Exercice de DM
13 messages
- Page 1 sur 1
Re: Exercice de DM
Bonjour,
tu calcules la dérivée, fais le tableau de variations, vois qu'il y a bien 3 valeurs qui annulent ta fonction et encadre ces valeurs à 0,1 près, comme on te le demande, en t'aidant de la calculatrice.
tu calcules la dérivée, fais le tableau de variations, vois qu'il y a bien 3 valeurs qui annulent ta fonction et encadre ces valeurs à 0,1 près, comme on te le demande, en t'aidant de la calculatrice.
Re: Exercice de DM
annick a écrit:Bonjour,
tu calcules la dérivée, fais le tableau de variations, vois qu'il y a bien 3 valeurs qui annulent ta fonction et encadre ces valeurs à 0,1 près, comme on te le demande, en t'aidant de la calculatrice.
Le problème c'est que l’encadrement obtenu est de [-10;-1] pou le premier [-1;1] pour le deuxième et [1;10] pour la troisième valeur (j'ai omis de préciser que la fonction était définie sur [-10;10]) nous n'avons pas le droit de nous aider graphiquement et je ne vois donc pas comment "rétrécir" ces encadrements
Re: Exercice de DM
Bjr
Concernant les solutions exactes c'est possible mais je ne sais pas si c'est à la portée de 1S .
En effet il faut connaitre un peu de trigonométrie.
Si tu poses) (c'est à dire l'angle qui a pour tangente
(c'est à dire l'angle qui a pour tangente 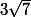 ) alors
) alors
) est une des solutions.
est une des solutions.
On peut alors calculer les 2 autres solutions qui sont
)
Tu pourras toujours comparer avec tes valeurs approchées.
Concernant les solutions exactes c'est possible mais je ne sais pas si c'est à la portée de 1S .
En effet il faut connaitre un peu de trigonométrie.
Si tu poses
On peut alors calculer les 2 autres solutions qui sont
Tu pourras toujours comparer avec tes valeurs approchées.
Re: Exercice de DM
aviateur a écrit:Bjr
Concernant les solutions exactes c'est possible mais je ne sais pas si c'est à la portée de 1S .
En effet il faut connaitre un peu de trigonométrie.
Si tu poses(c'est à dire l'angle qui a pour tangente
) alors
est une des solutions.
On peut alors calculer les 2 autres solutions qui sont
Tu pourras toujours comparer avec tes valeurs approchées.
En effet c'est quelque chose que je n'ai jamais vu
 je pense qu'il doit y avoir un moyen avec les outils a ma disposition, surement des dérivées mais en essayant avec je n'ai rien trouver de concluant
je pense qu'il doit y avoir un moyen avec les outils a ma disposition, surement des dérivées mais en essayant avec je n'ai rien trouver de concluantRe: Exercice de DM
Non on n'utilise pas la dérivée mais la formule = 4 cos ^3 (u) - 3 cos (u)) qui permet de résoudre l'équation. ça doit se faire en 1S pourvu que la fonction cosinus (et sinus) soit connue.
qui permet de résoudre l'équation. ça doit se faire en 1S pourvu que la fonction cosinus (et sinus) soit connue.
De toute façon c'est clair qu'on ne te demande pas ça mais une résolution numérique.
A 0.1 près, avec une calculette tu appliques la méthode de Dichotomie.
De toute façon c'est clair qu'on ne te demande pas ça mais une résolution numérique.
A 0.1 près, avec une calculette tu appliques la méthode de Dichotomie.
Re: Exercice de DM
bonjour,
De quel moyen informatique disposes-tu ? ordi, calculatrice ? avec quel langage ?
tu as au moins trois méthodes pour résoudre ces équations:
- balayage
-dichotomie
- méthode de Newton
De quel moyen informatique disposes-tu ? ordi, calculatrice ? avec quel langage ?
tu as au moins trois méthodes pour résoudre ces équations:
- balayage
-dichotomie
- méthode de Newton
Modifié en dernier par mathelot le 05 Mar 2019, 19:15, modifié 1 fois.
Re: Exercice de DM
aviateur a écrit:Non on n'utilise pas la dérivée mais la formulequi permet de résoudre l'équation. ça doit se faire en 1S pourvu que la fonction cosinus (et sinus) soit connue.
De toute façon c'est clair qu'on ne te demande pas ça mais une résolution numérique.
A 0.1 près, avec une calculette tu appliques la méthode de Dichotomie.
Je vois, merci bien je vais voir ce que je peux faire de vos précieuses information
Re: Exercice de DM
mathelot a écrit:bonjour,
De quel moyen informatique disposes-tu ? ordi, calculatrice ? avec quel langage ?
tu as au moins trois méthodes pour résoudre ces équations:
- balayage
-dichotomie
- méthode de Newton
Et bien la seule contrainte et de trouver par calcul, donc tout ce qui est graphique on oublie (je dispose de PC, calculatrice et langage arithmétique? ce n'est ni du python ni du scratch ou autre. La dichotomie ne me dis rien, le prof nous a déjà parler de la méthode de newton cependant nous ne l'avons pas encore vu, et je connais le balayage cependant je ne vois pas comment l'appliquer ici
Re: Exercice de DM
A mon avis vu la précision demandée et avec une calculette, la Dichotomie est le plus rapide:
Par exemple tu as une racine entre 1 et 2. Soit a cette racine ds I=[1,2]
f(1)= -9 f(2)=7.
1. Tu coupe en 2. Le milieu c'est m=3/2=1.5 et f(1,5)= -5.5 dc

2. On recommence tu coupes en 2 m=(1.5+2)/2=1.75 et
f(1.75)= -0. 5625
dc

3. m=1.875 et f(1.75)=2.86
donc
I;e avec cette méthode du divise la longueur de l'intervalle par 2 à chaque étape.
Par exemple tu as une racine entre 1 et 2. Soit a cette racine ds I=[1,2]
f(1)= -9 f(2)=7.
1. Tu coupe en 2. Le milieu c'est m=3/2=1.5 et f(1,5)= -5.5 dc
2. On recommence tu coupes en 2 m=(1.5+2)/2=1.75 et
f(1.75)= -0. 5625
dc
3. m=1.875 et f(1.75)=2.86
donc
I;e avec cette méthode du divise la longueur de l'intervalle par 2 à chaque étape.
Re: Exercice de DM
J'avais utilisé la dérivée pour prouver d'après le tableau de variation qu'il y avait bien 3 solutions à cette équation et pour pouvoir aboutir à la méthode de dichotomie.
Re: Exercice de DM
re,
les trois intervalles contenant les racines sont par exemple

par exemple, pour le premier intervalle:
=-9) et
et =7)
la fonction polynômiale f est continue. Si les deux images f(-2) et f(-1) ont des signes différents, l'un négatif, l'autre positif, alors la fonction f s'annule dans l'intervalle. C'est une conséquence d'un théorème de classe de terminale, appelé TVI (théorème des valeurs intermédiaires).
pour la méthode de Newton, de calcul de valeurs approchées d'une racine d'un polynôme,
on démarre avec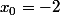
La courbe va rencontrer l'axe des x (l'axe des abscisses). On remplace la courbe par sa tangente au point d'abscisse . La droite tangente a pour équation
. La droite tangente a pour équation
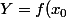+f'(x_0)(X-x_0).)
Cette tangente coupe l'axe des abscisses au point d'abscisse .
. vérifie l'égalité:
vérifie l'égalité:
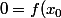+f'(x_0)(x_1-x_0))
soit
}{f'(x_0)})
 est une première valeur approchée de la racine.
est une première valeur approchée de la racine.
On recommence le procédé avec à la place de
à la place de  . On construit , de proche en proche, la suite (x_n) définie par:
. On construit , de proche en proche, la suite (x_n) définie par:
}{f'(x_n)})
Cette suite converge très rapidement vers la racine.
ici cette suite vaut , pour le premier intervalle:
})
et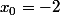
En pseudo-code, l'algorithme est donc:
-2 ---> X (on renseigne X à la valeur -2)
0 ----> I
TANT-QUE I<100
}) ----->X
----->X
I+1 ----> I
FIN-TANT-QUE
AFFICHER X
on trouve X -1.68878
-1.68878
ici, la méthode de Newton converge très très mal.Fréquement, au bout de cinq opérations,
on trouve dix décimales exactes. Ici, j'ai itéré cent fois pour obtenir une bonne approximation.
les trois intervalles contenant les racines sont par exemple
par exemple, pour le premier intervalle:
la fonction polynômiale f est continue. Si les deux images f(-2) et f(-1) ont des signes différents, l'un négatif, l'autre positif, alors la fonction f s'annule dans l'intervalle. C'est une conséquence d'un théorème de classe de terminale, appelé TVI (théorème des valeurs intermédiaires).
pour la méthode de Newton, de calcul de valeurs approchées d'une racine d'un polynôme,
on démarre avec
La courbe va rencontrer l'axe des x (l'axe des abscisses). On remplace la courbe par sa tangente au point d'abscisse
Cette tangente coupe l'axe des abscisses au point d'abscisse
soit
On recommence le procédé avec
Cette suite converge très rapidement vers la racine.
ici cette suite vaut , pour le premier intervalle:
et
En pseudo-code, l'algorithme est donc:
-2 ---> X (on renseigne X à la valeur -2)
0 ----> I
TANT-QUE I<100
I+1 ----> I
FIN-TANT-QUE
AFFICHER X
on trouve X
ici, la méthode de Newton converge très très mal.Fréquement, au bout de cinq opérations,
on trouve dix décimales exactes. Ici, j'ai itéré cent fois pour obtenir une bonne approximation.
Modifié en dernier par mathelot le 05 Mar 2019, 22:08, modifié 1 fois.
Re: Exercice de DM
Je vois tout est beaucoup plus clair maintenant, merci a vous trois c'est très sympa de vous être arrêté sur mon problème je vais enfin pouvoir avancer, sur ce je vous souhaite une agréable nuit et encore merci c'était tres instructif 

13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
