Ca a l'air vraiment urgent à ce que je vois...
Bon attends, j'écris.
Exercice sur suites et somme TS
37 messages
- Page 2 sur 2 - 1, 2
par terminales » 12 Oct 2012, 21:59
Kikoo <3 Bieber a écrit:Ca a l'air vraiment urgent à ce que je vois...
Bon attends, j'écris.
oh merci t'es un ange de m'avoir repondu! je te dois ma vie!
par terminales » 12 Oct 2012, 22:12
terminales a écrit:oh merci t'es un ange de m'avoir repondu! je te dois ma vie!
j'espere que tu ne m'a pas laissé tombé :triste:
par Kikoo <3 Bieber » 12 Oct 2012, 22:23
Tu as pu calculer les 5 premiers termes de la suite 
.
A partir de là, le but est d'essayer de trouver une formule pour et ce en fonction de n.
Le truc qu'est cool, c'est qu'on ne te demande pas de la prouver, on va pouvoir y aller bourrin.
Moi je trouve :
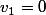
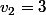
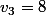
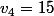
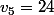
On remarque facilement que
Pas besoin de justifier donc on continue.
On te demande d'en déuire une formule pour
.
Tu donnes alors
Bon, cette étape de faite, on passe à la récurrence, que je vais te rédiger, mais ce sera la seule fois :
On montre qu'au premier rang n=1, la formule supputée ci-dessus est vraie. En effet, la somme de 1 à 1 de k(k-1) multipliée par 1/1 donne 0 et (1²-1)/3=0.
Supposons qu'elle soit vraie à un certain rang n supérieur à 1 (au sens large).
Montrons qu'elle est vraie au rang suivant n+1, c'est-à-dire que=\frac{(n+1)^2-1}{3})
Or nous savons que=\frac{1}{n+1}\(\sum_{k=1}^{n}k(k-1)\, +\,(n+1)n\)=n+\frac{1}{n+1}\sum_{k=1}^{n}k(k-1))
.
Or, par hypothèse de récurrence, on a=n\frac{(n^2-1)}{3})
donc :
=n+\frac{n}{3(n+1)}(n^2-1)=\frac{n(n^2-1+3n+3)}{3(n+1)}=\frac{n(n+1)(n+2)}{3(n+1)}=\frac{n(n+2)}{3}=\frac{(n+1)^2-1}{3})
Donc cela clôt la récurrence.
Bonne soirée
A partir de là, le but est d'essayer de trouver une formule pour
Le truc qu'est cool, c'est qu'on ne te demande pas de la prouver, on va pouvoir y aller bourrin.
Moi je trouve :
On remarque facilement que
Pas besoin de justifier donc on continue.
On te demande d'en déuire une formule pour
Tu donnes alors
Bon, cette étape de faite, on passe à la récurrence, que je vais te rédiger, mais ce sera la seule fois :
On montre qu'au premier rang n=1, la formule supputée ci-dessus est vraie. En effet, la somme de 1 à 1 de k(k-1) multipliée par 1/1 donne 0 et (1²-1)/3=0.
Supposons qu'elle soit vraie à un certain rang n supérieur à 1 (au sens large).
Montrons qu'elle est vraie au rang suivant n+1, c'est-à-dire que
Or nous savons que
Or, par hypothèse de récurrence, on a
Donc cela clôt la récurrence.
Bonne soirée
par terminales » 12 Oct 2012, 22:24
Kikoo <3 Bieber a écrit:Tu as pu calculer les 5 premiers termes de la suite
A partir de là, le but est d'essayer de trouver une formule pour
Le truc qu'est cool, c'est qu'on ne te demande pas de la prouver, on va pouvoir y aller bourrin.
Moi je trouve :
On remarque facilement que
Pas besoin de justifier donc on continue.
On te demande d'en déuire une formule pour
Tu donnes alors
Bon, cette étape de faite, on passe à la récurrence, que je vais te rédiger, mais ce sera la seule fois :
On montre qu'au premier rang n=1, la formule supputée ci-dessus est vraie. En effet, la somme de 1 à 1 de k(k-1) multipliée par 1/1 donne 0 et (1²-1)/3=0.
Supposons qu'elle soit vraie à un certain rang n supérieur à 1 (au sens large).
Montrons qu'elle est vraie au rang suivant n+1, c'est-à-dire que
Or nous savons que
Or, par hypothèse de récurrence, on a
Donc cela clôt la récurrence.
Bonne soirée
et la question d je fais comment aide moi merci bcp
par Kikoo <3 Bieber » 12 Oct 2012, 22:28
Un petit effort voyons !
Nous avons=\frac{1}{n}\(\sum_{k=1}^n (k^2-k)\)=\frac{1}{n}\(\sum_{k=1}^n k^2-\sum_{k=1}^n k\))
Et le reste c'est du cours, c'est-à-dire qu'on t'autorise à le recopier
Re-bonne nuit
Nous avons
Et le reste c'est du cours, c'est-à-dire qu'on t'autorise à le recopier
Re-bonne nuit
par terminales » 12 Oct 2012, 22:35
Kikoo <3 Bieber a écrit:Un petit effort voyons !
Nous avons
Et le reste c'est du cours, c'est-à-dire qu'on t'autorise à le recopier
Re-bonne nuit
non attends j'ai pas compris
par Kikoo <3 Bieber » 12 Oct 2012, 22:37
Allez fais vite, j'ai DS demain.
Qu'est-ce que t'as pas compris ?
Qu'est-ce que t'as pas compris ?
par terminales » 12 Oct 2012, 22:38
Kikoo <3 Bieber a écrit:Allez fais vite, j'ai DS demain.
Qu'est-ce que t'as pas compris ?
comment tu fais apres pour repondre à la question je suis pas ton raisonnement
par terminales » 12 Oct 2012, 22:42
terminales a écrit:comment tu fais apres pour repondre à la question je suis pas ton raisonnement
hein t'es parti? :triste:
par terminales » 12 Oct 2012, 22:48
Kikoo <3 Bieber a écrit:Ben c'est de la cuisine :
merci merci merci mille merci et dsl de t'avoir retenu pour ton ds de demain bonne chance et bonne nuit :we:
par Kikoo <3 Bieber » 12 Oct 2012, 22:51
terminales a écrit:merci merci merci mille merci et dsl de t'avoir retenu pour ton ds de demain bonne chance et bonne nuit :we:
Muchas gracias, bonne continuation pour la suite
par Kikoo <3 Bieber » 13 Oct 2012, 12:02
Certes Euler07 :/ Mais bon, j'ai vu que ça bloquait toute la soirée et comme personne ne répondait, je me suis décidé à faire une exception... Je pouvais pas me permettre de passer mon temps à expliquer
37 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :