Exercice sur produit scalaire 2
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 15:35
par Ugodu13112 » 28 Fév 2013, 15:35
Ah d'accord et pour la question 3 ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 15:37
par ampholyte » 28 Fév 2013, 15:37
Donne moi l'équation cartésienne du cercle que tu obtiens, que je puisse vérifier avant de passer à la suite.
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 15:42
par Ugodu13112 » 28 Fév 2013, 15:42
x^2 + y^2 + 4x - 10y - 55 = 0 ??
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 15:45
par Ugodu13112 » 28 Fév 2013, 15:45
c'est -51 plutot *

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 15:48
par ampholyte » 28 Fév 2013, 15:48
Tu dois laisser sous la forme que je t'ai donné plus haut :
D'ailleurs ne voyant pas apparaitre le racine de 80, je doute de ta solution.
(x - xi)² + (y - yi)² = R²
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 15:55
par Ugodu13112 » 28 Fév 2013, 15:55
(x + 2)^2 + (y - 5 )^2 = 80
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 15:58
par Ugodu13112 » 28 Fév 2013, 15:58
C'est ca ?? Et pour la question 3 ??

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 15:58
par ampholyte » 28 Fév 2013, 15:58
Alors presque mais ce n'est pas ça.
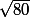
est le diamètre donc
^2 + (y - 5)^2 = (\frac{\sqrt{80}}{2})^2)
(x + 2)² + (y - 5)² = 20
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 15:59
par Ugodu13112 » 28 Fév 2013, 15:59
J'ai pas compris c'est racine de 80 divisé par 2 ??

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 16:00
par ampholyte » 28 Fév 2013, 16:00
3) Soit M(x; y) un point de la tangente au cercle passant par B alors on a
On peut donc écrire le produit scalaire suivant :

Effectue ce calcul et tu auras ta réponse.
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 16:06
par Ugodu13112 » 28 Fév 2013, 16:06
MB.IB=0 ok mais a quoi ca nous sert pour l'équation cartésienne ?
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 16:13
par Ugodu13112 » 28 Fév 2013, 16:13
Ampholyte comment on fait maintenant ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 16:48
par ampholyte » 28 Fév 2013, 16:48
Comme l'équation cartesienne s'écrit ay + bx + c = 0, cela va te permettre de trouver cette équation.
Trouve les coordonnées de MB et de IB et calcule le produit scalaire.
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 16:50
par Ugodu13112 » 28 Fév 2013, 16:50
2x + 4y - 28 = 0 ??

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 17:05
par ampholyte » 28 Fév 2013, 17:05
Peux-tu détailler ton calcul.
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 17:08
par Ugodu13112 » 28 Fév 2013, 17:08
MB (-4-x;9-y) IB (-2;4)
MB.IB = (-4-x) x (-2) - (9-y) x 4
MB.IB = 8 + 2x - 36 + 4y
MB.IB = 2x + 4y - 28
voila

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 28 Fév 2013, 17:11
par ampholyte » 28 Fév 2013, 17:11
C'est ça parfait :)
-
Ugodu13112
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2013, 11:56
-
 par Ugodu13112 » 28 Fév 2013, 17:13
par Ugodu13112 » 28 Fév 2013, 17:13
Cool on a finit merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
