Exercice sur les valeurs intérmédiaires

[fpaco]

Bonjour, voici un exo sur lequel je bloque :
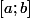
Soit continue sur tel que
Montrer que admet un point fixe sur

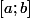
Je sais que pour montrer que f admet un point fixe, il faut montrer queil existe
tel que
Cependant je suis complètement bloqué.
Un peu d'aide serai la bien venue.
Merci

[phyelec]

Bonjour,

f est continue , on créer la fonction g(x)=f(x)-x.
g est continue sur [a;b] puisque f l'est.

f est continue sur [a;b] donc f est bornée sur [a;b], f prend au moins une fois toutes les valeurs comprises entre le minimum m et le maximum M.

on a [a;b] inclus dans f( [a;b]) :
donc il existe une valeur c appartenant à [a;b], telle que f(c)=a, donc g(c)=f(c)-c=a-c est inférieur où égal à 0
donc il existe une valeur d appartenant à [a;b], telle que f(d)=b, donc g(d)=f(d)-d=b-d est supérieur où égal à 0

je vous laisse finir en appliquant le théorème des valeurs intermédiaire.