Bonsoir à tous je dois rendre un exercice sur les sommes ét il m'en manque 2 que j'arrive pas à faire j'aimerais bien que vous m'aidiez :
n
E (-1)^k+1 x 2^n-k
k=0
n
E (n combinaison k) / 5^2k+1
k=0
Merci
Exercice sur les sommes (prépa ecs)
7 messages
- Page 1 sur 1
Re: Exercice sur les sommes (prépa ecs)
Merci beaucoup mais j'aimerai avoir les détails pour pouvoir mieux comprendre
Re: Exercice sur les sommes (prépa ecs)
Bonsoir,
Pour détailler le calcul de Razes :
1- Sors un de ta somme (comme ça il te reste du
de ta somme (comme ça il te reste du ^k) )
)
2- Sors le : il te reste du
: il te reste du ^k\cdot 2^{-k}=\left( -\frac{1}{2}\right)^k)
Pour détailler le calcul de Razes :
1- Sors un
2- Sors le
Re: Exercice sur les sommes (prépa ecs)
Ah oui Cest Bon j'ai compris le raisonnement dois je maintenant appliquer la formule de la somme géométrique ????
Re: Exercice sur les sommes (prépa ecs)
Pour la deuxième, il suffit de remarquer que 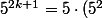^k) . Ainsi
. Ainsi
1- Sors un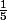 de ta somme
de ta somme
2- Il te reste à calculer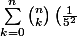^k=\sum_{k=0}^n\binom{n}{k}\left(\frac{1}{25}\right)^k\cdot 1^{n-k}) ...
...
Oui
1- Sors un
2- Il te reste à calculer
Dydy13 a écrit:Ah oui Cest Bon j'ai compris le raisonnement dois je maintenant appliquer la formule de la somme géométrique ????
Oui
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
