Exercice sur les limites et fonction

[Serra-Tayanami]

Bonjour,

J'ai fais l'exercice... Je joins ce que j'ai fais, pouvez-vous me dire s'il vous plait si mes calculs sont justes, la droite est à la fin... merci =)

[Cheche]

Bonjour :)

1] Tu n'as pas commencé ton exercice en vérifiant si ta fonction était bien définie sur :(:(

2] Question 1.a :

Tu peux nous expliquer le calcul de tes limites car il y a des passages que je ne comprends vraiment pas.

[Ramanujan71]

Tangeante :lol3:

[Serra-Tayanami]

Bonjour :)

1] Tu n'as pas commencé ton exercice en vérifiant si ta fonction était bien définie sur :(:(

2] Question 1.a :

Tu peux nous expliquer le calcul de tes limites car il y a des passages que je ne comprends vraiment pas.

Bonjour, merci pour votre réponse.

Je ne sais pas comment faire pour vérifier si la fonction se trouve bien sur I... Quel passage ne comprenez-vous pas ?

Merci

[Cheche]

Si je dis que je ne comprends pas, c'est qu'il y a surement des erreurs :(.

Pour l'ensemble de définition, on sait que :

ln(X) est définie sur X > 0
Donc la question que l'on peut commencer à se poser et de savoir si :

Pour tout

Ensuite,





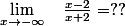
Et essayes de nous expliquer comment tu t'y prends pour que l'on détecte tes éventuelles erreurs.
P.S. : Hésites pas à utiliser les balises TEX pour faciliter l'écriture de tes formules
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php

[Serra-Tayanami]

Si je dis que je ne comprends pas, c'est qu'il y a surement des erreurs :(.

Pour l'ensemble de définition, on sait que :

ln(X) est définie sur X > 0
Donc la question que l'on peut commencer à se poser et de savoir si :

Pour tout

Ensuite,





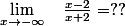
Et essayes de nous expliquer comment tu t'y prends pour que l'on détecte tes éventuelles erreurs.
P.S. : Hésites pas à utiliser les balises TEX pour faciliter l'écriture de tes formules
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php

J'ai pas mal de lacune en math, lorsque j'ai un exercice à faire, je me base sur une correction d'un exercice similaire.

Pour la 1ère question, dans mon livre de math, il y'avait un exo corrigé qui permettait de déterminer des fonctions aux bornes de leur définition... Je me suis servi de cette exercice corrigé pour faire cette question...

Voici l'exercice dont je viens de vous parler...

sur ]0;[

la correction était:
=

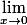
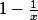
donc =



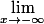
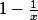
= 1

donc = 1


Voilà, je me suis basée sur cette exercice =/

[Cheche]

c'est totalement faux.

Pour x= 1/2,

On obtient : 1 - 1/(1/2) = 1-2 = -1 et ln(-1) n'existe pas.

- Il est préférable de réfléchir que d'essayer de faire du copier-coller.

- Est-ce que tu connais la représentation graphique de 1/x ?? de ln(x) ??
Il faudra commencer par cela et voir sur la représentation graphique, comment
on voit les informations concernant les limites.

[Serra-Tayanami]

c'est totalement faux.

Pour x= 1/2,

On obtient : 1 - 1/(1/2) = 1-2 = -1 et ln(-1) n'existe pas.

- Il est préférable de réfléchir que d'essayer de faire du copier-coller.

- Est-ce que tu connais la représentation graphique de 1/x ?? de ln(x) ??
Il faudra commencer par cela et voir sur la représentation graphique, comment
on voit les informations concernant les limites.

je pense que la représentation graphique de 1/x est celle ci:


quand à celle de la courbe est croissante... elle commence à froller l'axe des ordonnées sous l'axe des abscisses, puis, elle dépasse l'axe des abscisses... c'est bien ça ?

[Cheche]

parfait :).
Oui, elle dépasse l'axe des abscisses en x=1 pour rappel.
Car ln(1)=0

[Cheche]

Revenons à ce que l'on cherchait :



Étape 1 :

Démontrer que : Pour tout

Étape 2 :



Étape 3 :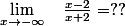

[Serra-Tayanami]

Revenons à ce que l'on cherchait :



Étape 1 :

Démontrer que : Pour tout

Étape 2 :



Étape 3 :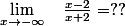

Pour l'étape 1, je ne suis pas sûre, mais est-ce que c'est ceci:

[Cheche]

Étape 1 :

Pourquoi tu as essayé de dériver ??
Pour tout , x-2 0.
CQFD.

Étape 2 :