Exercice sur les familles de fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nanadvl27
- Messages: 5
- Enregistré le: 07 Déc 2013, 13:06
-
 par nanadvl27 » 07 Déc 2013, 13:31
par nanadvl27 » 07 Déc 2013, 13:31
Bonjour,
J'ai un exercice de maths à faire sur les fonctions mais j'ai beaucoup de mal, pouvez vous m'aider.
Voici l'énoncé :
Pour tout k réel, on définit la fonction fk sur )0,+oo( par fk(x)=((kx+1)/x)*exp(x)
On suppose k<0
a. Déterminer les limites de fk en 0 et en +oo.
b. Calculer f'k(x) et déterminer selon les valeurs de k, le nombre de solutions de f'k(x=0)
Pour la limite quand x tend vers 0 et k<0 j'ai fais :
- lim kx=0
- lim 1/x=+oo
- lim exp(x)= -oo (celle là je ne suis pas sur, c'est peut-être 1)
et après je ne sais pas vraiment quoi faire.
Le prof nous a dit que l'on devait trouver que kx+1/x tend vers k et que exp(x) tend vers +o.
Pour la limite quand x tend vers +oo et k<0,
- lim kx=-oo
- lim 1/x=-oo
- lim exp(x)=+oo
Pour la dérivée le prof nous a dit qu'il fallait faire u*v, mais je pense qu'il faut déjà faire u/v et après u*v.
Je sais que l'on doit trouver f'k(x)= exp(x)*((kx^2+x-1)/x^2).
Merci d'avance pour votre aide.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 07 Déc 2013, 14:23
par Carpate » 07 Déc 2013, 14:23
-
nanadvl27
- Messages: 5
- Enregistré le: 07 Déc 2013, 13:06
-
 par nanadvl27 » 07 Déc 2013, 18:40
par nanadvl27 » 07 Déc 2013, 18:40
Ok merci beaucoup,
Est ce que vous pouvez m'aider pour les limites svp ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 07 Déc 2013, 19:05
par mcar0nd » 07 Déc 2013, 19:05
Salut, reprends l'expression de ta fonction, qui est
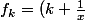e^x)
.
On te dit qu'un suppose k strictement négatif.
Que vaut
)
?
ET que vaut

?
-
nanadvl27
- Messages: 5
- Enregistré le: 07 Déc 2013, 13:06
-
 par nanadvl27 » 08 Déc 2013, 10:51
par nanadvl27 » 08 Déc 2013, 10:51
lim (k+1/x) vaut +oo
et lim epx vaut aussi +oo
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Déc 2013, 11:29
par Carpate » 08 Déc 2013, 11:29
nanadvl27 a écrit:lim (k+1/x) vaut +oo
et lim epx vaut aussi +oo
Tu parles de quelle limite quand
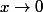
ou
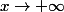
?
=(k+\frac{1}{x})e^x)
En

,

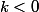
donc
)

En

,

,

donc
 \rightarrow ....)
-
nanadvl27
- Messages: 5
- Enregistré le: 07 Déc 2013, 13:06
-
 par nanadvl27 » 08 Déc 2013, 12:31
par nanadvl27 » 08 Déc 2013, 12:31
C'était pour x tend vers 0.
Pour trouver le nombre de solution de f'k(x)=0 je fais comment, j'ai un polynome en haut de la fraction mais je ne sais pas comment faire pour pouvoir l'utiliser....
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Déc 2013, 13:58
par Carpate » 08 Déc 2013, 13:58
nanadvl27 a écrit:C'était pour x tend vers 0.
Pour trouver le nombre de solution de f'k(x)=0 je fais comment, j'ai un polynome en haut de la fraction mais je ne sais pas comment faire pour pouvoir l'utiliser....
=\frac{kx^2+x-1}{x^2}.e^x=0)
Equation produit :
(\frac{1}{x^2})(e^x)=0)
a)

b)

est-ce possible ?
c)
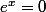
est-ce possible ?
-
nanadvl27
- Messages: 5
- Enregistré le: 07 Déc 2013, 13:06
-
 par nanadvl27 » 08 Déc 2013, 17:17
par nanadvl27 » 08 Déc 2013, 17:17
Non les deux sont impossible.
Pour le calcul de delta je trouve 1-4k, il faut que je fasse comment pour trouver les solutions ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Déc 2013, 18:57
par Carpate » 08 Déc 2013, 18:57
nanadvl27 a écrit:Non les deux sont impossible.
Pour le calcul de delta je trouve 1-4k, il faut que je fasse comment pour trouver les solutions ?

Non,

Ecris les solutions en fonctions du signe de

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
