Exercice sur les entiers
2 messages
- Page 1 sur 1
Re: exercice sur les entiers
par jonses » 08 Oct 2019, 05:56
Salut,
Je ne sais pas si tu as vu la fonction logarithme et la fonction exponentielle. Quand j'étais au lycée il y a environ 7-8 ans, on le voyait du coup je suppose que tu connais.
Déjà éliminons le cas évident :
: 
Pour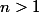
: je passe au logarithme :
^n (1+\frac{1}{n})) = n. ln(1-\frac{1}{n^2}) + ln(1+\frac{1}{n}))
l'étude de la fonction
définie par :
 = ln(1+x)-x)
montre facilement que \leq x)
avec égalité seulement en 0
On applique cela à notre cas, ce qui donne :
 + ln(1+\frac{1}{n} )< n.(\frac{-1}{n^2}) + \frac{1}{n} = 0)
En passant tout à l'exponentiel :
^n (1+\frac{1}{n})< 1)
Je ne sais pas si tu as vu la fonction logarithme et la fonction exponentielle. Quand j'étais au lycée il y a environ 7-8 ans, on le voyait du coup je suppose que tu connais.
Déjà éliminons le cas évident :
Pour
l'étude de la fonction
montre facilement que
On applique cela à notre cas, ce qui donne :
En passant tout à l'exponentiel :
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :