Exercice sur les dérivés.

[plunulleenmathquemoiyapas]

Bonjour à tous je viens vers vous aujourd'hui car j'ai de réelles difficultés à comprendre cet exercice sur les dérivés. Pourriez-vous m'aider s'il vous plaît j'ai essayé mais c'est exercice me semble vraiment difficile . Je suis en première ES

Voici l'énoncé :


Le bénéfice, en centaines d'euros, réalisé par une société pour un nombre X d'articles vendus est donné par la relation :

B(x) = - 0,04x(au carré) + 10,8x -104

A)Étudier les variations de la fonction bénéfice B sur l'intervalle [0;300]
B) en déduire le nombre d'articles correspondant à un bénéfice maximum. Quel est ce bénéfice ?
C) déterminer pour quelle quantité d'articles la société est bénéficiaire.

Merci beaucoup

[ampholyte]

Bonjour,

A) Afin d'étudier les variations de la fonction B(x), il y a 3 étapes :

1) Calculer B'(x) (la dérivée) sur [0; 300]

Pour rappel voici la dérivée d'une équation du second degré :

Soit a, b et c des rééls ;


Donc B'(x) = ....

2) Il faut étudier le signe de la dérivée c'est à dire résoudre B'(x) = 0 et B'(x) 0 (donc de faire le tableau de signe de B(x)

[plunulleenmathquemoiyapas]

Super un grand merci pour votre réponse claire, une dernière petite question pour pouvoir terminer dans les calcules :

B'(x)= 2 × (-0,0 4X) + 10,8
= -0,0 8X + 10,8 ?

[ampholyte]

Super un grand merci pour votre réponse claire, une dernière petite question pour pouvoir terminer dans les calcules :

B'(x)= 2 × (-0,0 4X) + 10,8
= -0,0 8X + 10,8 ?

C'est correct, tu peux continuer =).

[plunulleenmathquemoiyapas]

Ok super donc
B'(x)=0
-0,08x + 10,8 = 0
-0,08x = -10,8
X = (-10,8/-0,08) = 135

La je fais un tableau de variation comme :
X 0 135 300
Signe + 0 -
Sens. Croissant 0 Décroissant


B) on peut en déduire que le maximum est 135 car c'est le nombre le plus grand avant que la courbe ne deviennent décroissante

C) la société est bénéficiaire quand elle vend entre 0 et 135 articles [0;135] (je ne suis pas sûr que le 0 est dans l'intervalle.


Est ce juste ? (Encore mille mercis !)

[ampholyte]

Je suis ok pour A) et B)


Par contre pour C c'est un peu plus compliqué. Tu dois résoudre B(x) > 0 (avec la méthode du discriminant par exemple) et faire le tableau de signe.

Pour rappel :

Pour un polynôme de la forme ax² + bx + c

Si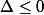 alors f(x) est du signe de a

Si alors f(x) est du signe de a à l'exterieur de ses racines et du signe de -a à l'intérieur de ses racines.

[plunulleenmathquemoiyapas]

Je suis ok pour A) et B)


Par contre pour C c'est un peu plus compliqué. Tu dois résoudre B(x) > 0 (avec la méthode du discriminant par exemple) et faire le tableau de signe.

Pour rappel :

Pour un polynôme de la forme ax² + bx + c

Si alors f(x) est du signe de a

Si alors f(x) est du signe de a à l'exterieur de ses racines et du signe de -a à l'intérieur de ses racines.

Ok c'est bon super je penses avoir compris j'ai calculé delta qui est au final égale a 100 donc racine carré de 100 = 10 donc delta est positif il détient deux solutions
X1= 10 et x2 = 260

Le tableau va donc changer cela va devenir

X 0 10 260 300

Signe - + -

S = [10;260]
Et de ce fait la société doit vendre entre 10 et 260 produit pour être bénéficiaire

[ampholyte]

Je suis d'accord avec ta réponse.

Par contre pourquoi le tableau va changer ?

Attention de ne pas confondre, le tableau de variation de B(x) qui contient le tableau de signe de B'(x) (la dérivée) et le tableau de signe de B(x).

Cela te donne 2 tableaux différents.

[plunulleenmathquemoiyapas]

D'accord d'accord bon beh super j'ai terminé alors ;) encore merci j'ai tout compris maintenant :)