Exercice sur les algorithmes seconde
12 messages
- Page 1 sur 1
exercice sur les algorithmes seconde
L’algorithme ci-dessous,écrit en python,renvoie une valeur y pour tout n entier naturel:
def: f(n):
i=n
y=0
While i>0
y=y+n
i=i-1
Return y
1)Expliquer pourquoi cet algorithme donne ,sans effectuer un produit le carrée de l’entier n
2)Proposer un algorithme qui calcule le cube d’un entier n toujours sans effectuer de produit
def: f(n):
i=n
y=0
While i>0
y=y+n
i=i-1
Return y
1)Expliquer pourquoi cet algorithme donne ,sans effectuer un produit le carrée de l’entier n
2)Proposer un algorithme qui calcule le cube d’un entier n toujours sans effectuer de produit
Re: exercice sur les algorithmes seconde
Pour montrer que l'algorithme se termine bien il faut exhiber un invariant de boucle, si on note 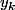 et
et 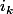 les valeurs des variables
les valeurs des variables  et
et  au bout de k itérations de la boucle while, on a
au bout de k itérations de la boucle while, on a 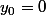 et
et 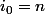 . Quelles relations de récurrence vérifient les suites
. Quelles relations de récurrence vérifient les suites ) et
et ) ?
?
Re: exercice sur les algorithmes seconde
Je n arrive toujours pas a comprendre comment a partir de 0 je peut justifier en fin de boucle avoir trouver le carree de l'entier n
Re: exercice sur les algorithmes seconde
j'aurais besoin d une explication plus détaillées pour les deux questions posées car je n'arrive pas a comprendre comment justifier mes réponses
Re: exercice sur les algorithmes seconde
D'après l'algorithme,  et
et  et l'invariant de boucle est
et l'invariant de boucle est  . En effet, l'initialisation est vraie puisque
. En effet, l'initialisation est vraie puisque 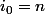 et
et 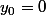 d'où
d'où  . Si on suppose l'égalité vraie au rang k, alors
. Si on suppose l'égalité vraie au rang k, alors 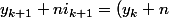+n(i_k-1)=y_k+ni_k=n^2) par hypothèse de récurrence. Il est clair que l'algorithme se termine puisque la suite
par hypothèse de récurrence. Il est clair que l'algorithme se termine puisque la suite ) est strictement décroissante donc la condition
est strictement décroissante donc la condition 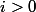 de la boucle while ne peut être indéfiniment vérifiée. Celle-ci s'arrête dès lors que
de la boucle while ne peut être indéfiniment vérifiée. Celle-ci s'arrête dès lors que 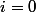 de sorte qu'en sortie
de sorte qu'en sortie  d'après l'invariant de boucle.
d'après l'invariant de boucle.
Re: exercice sur les algorithmes seconde
merci après réflexion j'ai réussi a trouver le même résultat pour la question 1 car pour y on trouve toujours 0
pour la question 2 qui permet de trouver le cube je suis obligée de changer mon algorithme ou je peux laisser le même en sachant qu'on trouvera toujours 0 ?
pour la question 2 qui permet de trouver le cube je suis obligée de changer mon algorithme ou je peux laisser le même en sachant qu'on trouvera toujours 0 ?
Re: exercice sur les algorithmes seconde
Cet algorithme permet de calculer le carré de l'entrée donc pour calculer le cube il faut bien sûr changer l'algorithme, qu'est-ce que tu entends par "pour y on trouve toujours 0" ?
Re: exercice sur les algorithmes seconde
je ne sais pas quoi changer dans l'algorithme pour trouver le cube car en fin de boucle on trouve toujours le resultat 0
on nous dit a la fin de l'algoritme "return y" et y=y+n donc y=0+0 on trouve toujours 0
on nous dit a la fin de l'algoritme "return y" et y=y+n donc y=0+0 on trouve toujours 0
Re: exercice sur les algorithmes seconde
Surtout pas, à quoi sert l'algorithme s'il renvoit toujours la même valeur ? d'autant plus que l'algorithme est censé renvoyer n², en plus la variable n est fixé puisque c'est un argument et que dans la fonction on ne modifie pas sa valeur. Le "=" en informatique n'a pas la même signification qu'en maths, l'instruction "y=y+n" signifie que la variable y prend la valeur y+n, autrement dit on rajoute n à y. La variable i agit comme un compteur, à chaque tour de la boucle while, on augmente y de n et on diminue i de 1. Puisque i vaut initialement n, la boucle while s'arrête lorsque i=0 donc après n passages dans la boucle while. Comme initialement y=0, les n passages de la boucles while ont pour en effet d'augmenter n fois la valeur de y par n, autrement dit, en sorti de boucle, la variable y a pour valeur n² et c'est cette valeur qui est renvoyée.
Re: exercice sur les algorithmes seconde
Merci pour l'explication je n'avais pas compris sa de cette façon
pour trouver le cube je doit trouver le nombre de n passages dans la boucle while afin que y=n au cube et i=0
pour trouver le cube je doit trouver le nombre de n passages dans la boucle while afin que y=n au cube et i=0
Re: exercice sur les algorithmes seconde
Pour avoir le cube il faut effectuer n² passages dans la boucle while, seulement si tu commences ton algorithme par "i=n*n", tu utilises une multiplication ce qui est interdit. Il y a plusieurs façons de procéder, tu peux par exemple appeler g ta fonction qui calcule le cube et faire référence à la fonction f de l'énoncé pour calculer n² puisqu'elle n'utilise pas de multiplication :
def g(n):
i=f(n)
y=0
....
Tu peux aussi utiliser une double boucle for :
def g(n):
y=0
for i in range(n):
for j in range(n):
y = y+n
return y
Chaque boucle for permet n passages donc tu as en tout n² appels de l'instruction "y=y+n".
def g(n):
i=f(n)
y=0
....
Tu peux aussi utiliser une double boucle for :
def g(n):
y=0
for i in range(n):
for j in range(n):
y = y+n
return y
Chaque boucle for permet n passages donc tu as en tout n² appels de l'instruction "y=y+n".
Re: exercice sur les algorithmes seconde
merci pour ton aide, je ne comprend rien aux algorithmes et grâce a ton aide j'ai appris pas mal de bases
Je pense pouvoir comprendre mon exercice avec tout sa
Je pense pouvoir comprendre mon exercice avec tout sa
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
