Exercice sur la dérivation 1ère S

[Shins]

Bonjour !
Alors voilà j'ai un petit problème avec un exercice sur la dérivation, nous venons de commencer le chapitre en classe, voici l'énoncé:
Soit f la fonction définie sur [-1 ; +infini [ par f(x)= ;)(x+1).
1. Démontrer que le taux d'accroissement de f entre 2 et 2+h est égal à 1 / ;)(h+3) + ;)(3) .

Pour cette question tout va bien pour le début, grâce à la formule du taux d'accroissement je trouve: (;)(h+3) - ;)3) / h .
Mais pour passer à la forme 1 / ;)(h+3) + ;)(3) je bloque. En essayant une ré-écriture par quantité conjuguée je trouve: 0 / ;)(h+3) + ;)(3) et je ne trouve pas comment retrouver bonne forme.

Merci d'avance !

[Math3matiqu3]

Le taux d’accroissement ( ) se calcule par la formule :

[Shins]

Oui je suis d'accord, mais l'exercice me demande une ré-écriture que je n'arrive pas à faire :(

[Carpate]

Bonjour !
Alors voilà j'ai un petit problème avec un exercice sur la dérivation, nous venons de commencer le chapitre en classe, voici l'énoncé:
Soit f la fonction définie sur [-1 ; +infini [ par f(x)= (x+1).
1. Démontrer que le taux d'accroissement de f entre 2 et 2+h est égal à 1 / (h+3) + (3) .

Pour cette question tout va bien pour le début, grâce à la formule du taux d'accroissement je trouve: (;)(h+3) - 3) / h .
Mais pour passer à la forme 1 / (h+3) + (3) je bloque. En essayant une ré-écriture par quantité conjuguée je trouve: 0 / (h+3) + (3) et je ne trouve pas comment retrouver bonne forme.

Merci d'avance !

Tu t'es trompé dans le calcul de de la forme
que vaut , et ?

[Shins]

;)(h+3) au carré = h+3
;)(3) au carré = 3
h+3 - 3 = h
et lorsque je souhaite réduire pour essayer de retrouver la forme que l'énoncé me demande, je trouve 0

[Math3matiqu3]

tu as maintenant simplifie en enlevant

[Shins]

Oui, c'est ce que j'ai voulu faire, mais je trouve 0 / ;)(h+3) + ;)(3) au lieu de 1 / ;)(h+3) + ;)(3) donc ça ne va pas

Merci de vos aides

[Carpate]

Oui, c'est ce que j'ai voulu faire, mais je trouve 0 / (h+3) + (3) au lieu de 1 / (h+3) + (3) donc ça ne va pas

Merci de vos aides

Ca vaudrait dire que
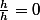
C'est énorme !!!

[Shins]

Comment je peux faire alors? :/

[Carpate]

Comment je peux faire alors? :/

Tu remplace h/h par 1 !!!
Qu'est-ce qui reste alors dans ton expression ?

[Shins]

Ahhh merci beaucoup j'ai pas pensé à ça, résultat je trouve la forme demandée

Merci beaucoup ! :)

[Math3matiqu3]

De rien mon ami :we:

Il faut juste que tu gardes en tête que " h " est un nombre très petit, qui dans des niveaux supérieurs, se nomme "epsilon" , même si il est très petit, il reste un nombre que tu peux manipuler et que tu dois prendre en considération ! n'est pas égal à 0 mais à 1