Exercice de 1°S - Suites

[Yruama]

Bonjour à tous !
Voici un exercice qui me pose problème depuis quelques temps :

U est la suite définie par son premier terme U0 et la relation de récurrence Un+1 = aUn + b pour tout n de N (entiers naturels) avec a et b réels fixés , sachant que a est différent de 0 .

1.Quelle est la nature de la suite lorsque a=1 ? Lorsque b = 0 ?

2.On suppose a différent de 1 .
a)Calculer en fonction de a et b l'abscisse Alpha du point d'intersection des droites d'équations : y = x et y = ax + b

b)Montrer que la suite V définie par tout n de N (entiers naturels) par
Vn = Un - Alpha est une suite géométrique .
Quelle est sa raison ?

c)Exprimer Vn puis Un en fonction de n et U0 .

J'ai répondu à la première question :
1.Lorsque a=1 la suite devient arithmétique puisque on a la forme
Un+1 = Un + b , et lorsque b=0 la suite est de forme Un = aUn , dans ce cas , c'est donc une suite géométrique .

C'est donc la question 2 qui me pose un sérieux problème .
Pour le a) j'ai essayais de faire a = ax +b ...

"Légende":
Lorsque j'écris Un+1 le n+1 se trouve en indice vers le bas du U ( je ne conner pas le terme exact mais je pense que vous comprenez ) .
A l'inverse Un + b , le n est toujours en indice mais le b ne l'est pas , d'ou le décalage que j'ai mis .
De même le U0, le 0 est en indice en dessous à droite du U .
(Lorsque j'écris aUn cela revient à écrire a(Un) .)

J'espère mettre fais comprendre ^^ .
D'avance pour votre aide !

[fatal_error]

salut,

concernant les indices tout d'abord :
tu peux ecrire u(n+1) qui est pe plus sûr. Mais comme, et c'est bien, tu sembles accorder de l'importance a la propreté des notations, tu peux aussi essayer en latex (balises TEX) :
u_{n+1} qui donne

pour la question 2, deux droites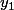 et 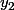se croisent signifie que

Dans ton énoncé, ca revient a resoudre
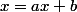, dont la solution est notée

[Yruama]

Salut ! Merci de ta réponse ; en effet j'ai déja résous a = ax + b mais je n'étais pas sur que ce soit la bonne réponse ...
Donc si j'ai bien compris le résultat est x = a/b ?


Merci de ton aide !

[fatal_error]

re,

ben deja, si tu ecris les étapes de calcul, c'est mieux pour nous, puis le cas échéant, tu peux remplacer x par la valeur que tu as trouvé et regarder si ca vérifie l'équation.

en remplacant par 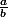, on trouve :

ce qui impose une condition sur a et b, alors que a et b sont quelconques.
Donc tu as une erreur.

[Yruama]

Si quelqu'un a une idée pour la suite je suis preneur ... ^^
A+