Exercice de suites avec conjectures...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 13 Fév 2012, 22:10
par Jota Be » 13 Fév 2012, 22:10
libellule03 a écrit:ok ! Mais du coup comment conjecturer un en fonction de n avec cette relation ?
On peut ainsi conjecturer que
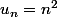
-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 22:25
par libellule03 » 13 Fév 2012, 22:25
Jota Be a écrit:On peut ainsi conjecturer que
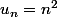
Ah d'accord! Cela fonctionne pour u1 =1² = 1 et u2 = 2² = 4 mais pas pour u3 avec qui l'on trouverait 9 mais moi je trouve u 3 = 13 ?
Je suis vraiment désolée de vous déranger autant ... :triste:
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 13 Fév 2012, 22:32
par Jota Be » 13 Fév 2012, 22:32
libellule03 a écrit:Ah d'accord! Cela fonctionne pour u1 =1² = 1 et u2 = 2² = 4 mais pas pour u3 avec qui l'on trouverait 9 mais moi je trouve u 3 = 13 ?
Je suis vraiment désolée de vous déranger autant ... :triste:
Haha mais je t'avais dit que tu ne t'étais pas trompée !
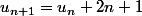
donc

Et non, tu me déranges pas, comme tu ne déranges pas les autres intervenants

-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 22:39
par libellule03 » 13 Fév 2012, 22:39
Jota Be a écrit:Haha mais je t'avais dit que tu ne t'étais pas trompée !
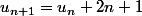
donc

Et non, tu me déranges pas, comme tu ne déranges pas les autres intervenants

Ha d'accord j'ai compris d'où venais mon erreur ^^. Merci
-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 22:51
par libellule03 » 13 Fév 2012, 22:51
libellule03 a écrit:Ha d'accord j'ai compris d'où venais mon erreur ^^. Merci
ET donc pour démontrer cette conjecture il faut montrer que (je nomme la conjecture ,un = n², vn)
vn = un
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 13 Fév 2012, 23:02
par Jota Be » 13 Fév 2012, 23:02
libellule03 a écrit:ET donc pour démontrer cette conjecture il faut montrer que (je nomme la conjecture ,un = n², vn)
vn = un
Non. Calcule juste

.
Indice : en prenant l'hypothèse de récurrence puis en prenant l'hypothèse issue de la conjecture.
-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 23:09
par libellule03 » 13 Fév 2012, 23:09
Jota Be a écrit:Non. Calcule juste

.
Indice : en prenant l'hypothèse de récurrence puis en prenant l'hypothèse issue de la conjecture.
Avec la récurrence:
u(n+1)-u(n)
= u(n)+2n+1-u(n)
=2n+1
Avec la conjecture:
u(n+1) -u(n)
= u(n+1) -n²
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 13 Fév 2012, 23:14
par Jota Be » 13 Fév 2012, 23:14
libellule03 a écrit:Avec la récurrence:
u(n+1)-u(n)
= u(n)+2n+1-u(n)
=2n+1
Avec la conjecture:
u(n+1) -u(n)
= u(n+1) -n²
T'y es presque.
En supposant que
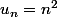
, que peut-on supposer pour

?
-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 23:15
par libellule03 » 13 Fév 2012, 23:15
Jota Be a écrit:T'y es presque.
En supposant que
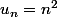
, que peut-on supposer pour

?
Que si u(n) = n² alors u(n+1) = n² +1
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 13 Fév 2012, 23:20
par Jota Be » 13 Fév 2012, 23:20
libellule03 a écrit:Que si u(n) = n² alors u(n+1) = n² +1
Hmmm non. Il faut plutôt voir
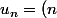^2)
et non pas
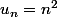
-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 23:22
par libellule03 » 13 Fév 2012, 23:22
Jota Be a écrit:Hmmm non. Il faut plutôt voir
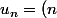^2)
et non pas
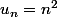
Donc c'est plutôt : u(n+1) = (n+1)²
Donc avec l'hyspothèse on obtient u(n+1) - u(n)
= (n+1)²-n²=
2n+1 comme la première avec la relation, et donc je pense que la demonstration est faite !

-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 13 Fév 2012, 23:30
par Jota Be » 13 Fév 2012, 23:30
libellule03 a écrit:Donc c'est plutôt : u(n+1) = (n+1)²
Exactement !
-
libellule03
- Membre Naturel
- Messages: 27
- Enregistré le: 13 Fév 2012, 20:12
-
 par libellule03 » 13 Fév 2012, 23:37
par libellule03 » 13 Fév 2012, 23:37
Jota Be a écrit:Exactement !
Eh bien je vous remercie pour votre aide précieuse !

Bonne soirée merci encore
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 101 invités