Exercice suite

[Tarabass911]

Bonjour,
J'ai un peu de mal a demarrer sur un exercice de math que j'ai à faire. J'aurais besoin d'un peu d'aide, merci.

ennoncé :

on considere la suite (Un) def par :
Uo=1
U(n+1)=(1+Un)^(1/2)
1) demontrer que la suite est croissante et majorée
2) qu'elles sont les valeur possible pour la limite de Un
3)Mq Un converge vers a = (1+5^1/2)/2

[Mikou]

1°)
On suppose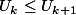 on applique f(x)= 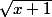quite est strictement croissante sur son interval. dou donc il ya donc heredité.
Si il existe k dans IN tq alors on aurait donc la suite est majorée par 2

2°) tt suite croissante majorée converge, la limite L ici doit verifier f(x)=x, f(x) doit etre continue en L

3°) je te laisse finir