Exercice suite récurrence
20 messages
- Page 1 sur 1
exercice suite récurrence
bonjour à tous,
Je trouve cet exercice très dur malgré le fait que je me débrouille pas mal en récurrence.
EXO:
Φ=solution positive de x²-x-1=0 soit le nombre d'or (1+V5/2) avec V = racine carré
On pose b0=2 et pour tout entier naturel n b(n+1)=Vb(n)+1 avec b(n)+1 sous la racine
1) Montrer par récurrence que pour tout entier n>=0, Φ=<b(n+1)=<bn=<2
2)en déduire que b(n) converge
3)Montrer que pour tout entier n>=0, 0=<b(n+1)-Φ=<1/3(b(n)-Φ)
4) en deduire que pr n>=1, O=<b(n)-Φ=<(1/3)^n
LIMITE DE b(n)?
5) déterminer un entier n2 tq si n>=n2 alors b(n)-Φ=<10^-6 en valeur absolue
Pour la 1 j'ai donc mis que b(n+2)=<b(n+1) et j'ai remplacé avec le reste mais cela ne mène à rien.
Je ne vois vraiment pas comment faire pour la suite ou il y a une démonstration, nous n'avons jamais vu de démos aussi dur, quelqu'un pour me donner une méthode svp!
Merci beaucoup
Je trouve cet exercice très dur malgré le fait que je me débrouille pas mal en récurrence.
EXO:
Φ=solution positive de x²-x-1=0 soit le nombre d'or (1+V5/2) avec V = racine carré
On pose b0=2 et pour tout entier naturel n b(n+1)=Vb(n)+1 avec b(n)+1 sous la racine
1) Montrer par récurrence que pour tout entier n>=0, Φ=<b(n+1)=<bn=<2
2)en déduire que b(n) converge
3)Montrer que pour tout entier n>=0, 0=<b(n+1)-Φ=<1/3(b(n)-Φ)
4) en deduire que pr n>=1, O=<b(n)-Φ=<(1/3)^n
LIMITE DE b(n)?
5) déterminer un entier n2 tq si n>=n2 alors b(n)-Φ=<10^-6 en valeur absolue
Pour la 1 j'ai donc mis que b(n+2)=<b(n+1) et j'ai remplacé avec le reste mais cela ne mène à rien.
Je ne vois vraiment pas comment faire pour la suite ou il y a une démonstration, nous n'avons jamais vu de démos aussi dur, quelqu'un pour me donner une méthode svp!
Merci beaucoup
Re: exercice suite récurrence
Salut,
Récurrence pour montrer que pour tout n entier naturel :
Initialisation : pas de problème
Hérédité :
Soit m entier naturel pour lequel
Exprime en remplaçant
en remplaçant 
Récurrence pour montrer que pour tout n entier naturel :
Initialisation : pas de problème
Hérédité :
Soit m entier naturel pour lequel
Exprime
Re: exercice suite récurrence
et bien c'est ce que j'ai fait mais j'obtiens b(n+2)=(VVb(n)+1+1)-Vb(n)+1, on ne peut pas contineur le calcul!
Re: exercice suite récurrence
Tes écritures avec des V sont illisibles
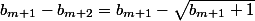
Maintenant tu utilises la quantité conjuguée
Maintenant tu utilises la quantité conjuguée
Re: exercice suite récurrence
ok en faisant ca je trouve b(n+1)/Vb(n+1)+1 et c'est positif donc b(n+2)>b(n+1) c'est ca?
Re: exercice suite récurrence
oui autant pour moi je trouve -1/b(n+1)+Vb(n+1)+1 mais c'est négatif.
je ne comprends pas pk on doit faire b(n+1)-b(n+2) et pas l'inverse. si b(n+1)-b(n+2) est négatif comme je l'ai trouvé ca veut dire que b(n+1)>b(n) or on nous demande de prouver exactement le contraire.
de plus comment prouver que b(n+1) est =<2 et est >=Φ
je ne comprends pas pk on doit faire b(n+1)-b(n+2) et pas l'inverse. si b(n+1)-b(n+2) est négatif comme je l'ai trouvé ca veut dire que b(n+1)>b(n) or on nous demande de prouver exactement le contraire.
de plus comment prouver que b(n+1) est =<2 et est >=Φ
Re: exercice suite récurrence
nikiboos28 a écrit:je ne comprends pas pk on doit faire b(n+1)-b(n+2) et pas l'inverse.
Peu importe.
Soit tu montres que b(n+1)-b(n+2) est positif, soit tu montres que b(n+2)-b(n+1) est négatif.
Re: exercice suite récurrence
D’accord mais mon calcul et bon ou pas et comment montrer que c’est plus petit que 2 ?
Et la suite svpp
Et la suite svpp
Re: exercice suite récurrence
Il faut chercher un peu ...
}{b_{m+1} + \sqrt{b_{m+1}+1}} = \frac{b_{m} - b_{m+1}}{b_{m+1} + \sqrt{b_{m+1}+1}})
Et on conclut grâce à l'hypothèse de récurrence.
Et on conclut grâce à l'hypothèse de récurrence.
Re: exercice suite récurrence
Mais si !
C'est l'hypothèse de récurence.
Hérédité :
Soit m entier naturel pour lequel , on montre qu'alors
, on montre qu'alors 
Il faut que tu revoies les démonstrations par récurrence.
C'est l'hypothèse de récurence.
Hérédité :
Soit m entier naturel pour lequel
Il faut que tu revoies les démonstrations par récurrence.
Re: exercice suite récurrence
nikiboos28 a écrit:des que cest un peu dur ya plus personne
Tu manques pas d'air toi !
Par récurrence, ça se fait très bien, c'est même plus facile que de montrer que b(n+1) < b(n).
Re: exercice suite récurrence
Soit =\sqrt{1+x}) ,
,  est croissante sur
est croissante sur 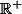 ,
, =\Phi) ,
, 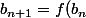) et
et =\sqrt{3}\leqslant 2) , avec ça tu peux normalement rédiger la récurrence.
, avec ça tu peux normalement rédiger la récurrence.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
