Exercice de Spécialité maths

[deadinsoul]

2) a_n*b_(n+1) - a_(n+1)*b_n = a_n(a_n+2b_n) - b_n(2a_n+3b_n) = (a_n)² + 2a_n*b_n - 2a_n*b_n - 3(b_n)² = (a_n)² - 3(b_n)²
Ensuite je peu remplacer par 2 et V3 ? ou pas ?

[Primperan]

Non, qu'est-ce que tu voudrais remplacer par 2 et ;)3 ?

Oublie le 2 et le ;)3 et simplifie donc ce que tu viens de trouver. Qu'est-ce que tu remarques?

[Primperan]

D'accord, je n'avais pas vu que tu l'avais déjà fait. Donc a_(n+1)² - 3b_(n+1)² = a_n² - 3b_n² .
On retombe sur l'expression de départ, mais avec n à la place de n+1 . Ca veut dire que si tu voulais calculer a_n - 3b_n, tu obtiendrais a_(n-1)² - 3b_(n-1)² n'est-ce pas ?
Et a_(n-1)² - 3b_(n-1)² = a_(n-2)² - 3b_(n-2)². On peut remonter jusqu'où comme ça?

[deadinsoul]

Non, qu'est-ce que tu voudrais remplacer par 2 et 3 ?

Oublie le 2 et le 3 et simplifie donc ce que tu viens de trouver. Qu'est-ce que tu remarques?

le a_n par 2 et b_n par V3 mais ce n'est pas ça.

(a_n)² - 3(b_n)²= (a_n)²-(V3b_n)²

[Primperan]

(On a posté presque en même temps, je reposte pour m'assurer que tu aies bien vu ce que j'ai dit.)

Tu vois où je veux en venir?

[deadinsoul]

D'accord, je n'avais pas vu que tu l'avais déjà fait. Donc a_(n+1) - 3b_(n+1) = a_n - 3b_n .
On retombe sur l'expression de départ, mais avec n à la place de n+1 . Ca veut dire que si tu voulais calculer a_n - 3b_n, tu obtiendrais a_(n-1) - 3b_(n-1) n'est-ce pas ?
Et a_(n-1) - 3b_(n-1) = a_(n-2) - 3b_(n-2). On peut remonter jusqu'où comme ça?

Jusqu'à a_0 - 3b_0 ?

[deadinsoul]

(On a posté presque en même temps, je reposte pour m'assurer que tu aies bien vu ce que j'ai dit.)

Tu vois où je veux en venir?

Donc on peut dire que (a_n)² - 3(b_n)² = 1 ?

[Primperan]

Oui tout à fait

[deadinsoul]

Oui tout à fait

En faite ce n'est pas dur mais il faut arriver a voir les choses.

(a_(n+1))/a_n = (2a_n + 3b_n)/a_n = 1/a_n ?

[Primperan]

Oui, les calculs ne sont pas compliqués, la difficulté c'est plutôt de voir les choses c'est vrai.

Tu dois prouver que a_n/b_n, a_(n+1)/an, b(n+1)/bn sont irréductibles, n'essaye surtout pas de les réduire ! :) Tu n'as même pas besoin de faire des calculs, rappelle-toi de ce qu'a dit Bézout...

[deadinsoul]

Oui, les calculs ne sont pas compliqués, la difficulté c'est plutôt de voir les choses c'est vrai.

Tu dois prouver que a_n/b_n, a_(n+1)/an, b(n+1)/bn sont irréductibles, n'essaye surtout pas de les réduire ! Tu n'as même pas besoin de faire des calculs, rappelle-toi de ce qu'a dit Bézout...

PGCD(a_n,b_n) doit être égal à 1 et idem pour les 2 autres fractions ?

[Primperan]

Oui c'est ça

[deadinsoul]

Oui c'est ça

Si a_n/b_n est irréductible PGCD(a_n;b_n)=1
On a donc : a_n*u + b_n*v = 1 d'après le théorème de bezou

[Primperan]

Oui, sauf que tu raisonnes à l'envers, il faut que tu partes de "a_n*u + b_n*v = 1" pour arriver à "a_n/b_n est irréductible". Tu as le bon raisonnement, mais fais-le dans l'autre sens

[Primperan]

Au fait pour la récurrence, tu as trouvé a_n et b_n, mais dans l'énoncé on te demandait aussi de montrer que "a_n et b_n sont des entiers positifs.". Il faut que tu le montres dans ta récurrence, c'est très rapide à faire ça prend une ou deux lignes, mais il faut le faire.

[deadinsoul]

D'accord, je n'avais pas vu que tu l'avais déjà fait. Donc a_(n+1)² - 3b_(n+1)² = a_n² - 3b_n² .
On retombe sur l'expression de départ, mais avec n à la place de n+1 . Ca veut dire que si tu voulais calculer a_n - 3b_n, tu obtiendrais a_(n-1)² - 3b_(n-1)² n'est-ce pas ?
Et a_(n-1)² - 3b_(n-1)² = a_(n-2)² - 3b_(n-2)². On peut remonter jusqu'où comme ça?

a_(n+1)² - 3_(n+1)² = a_n*b_(n+1) - a_(n+1)*b_n

Mais je ne voi pas comment vous pouvez dire que a_(n+1)² - 3b_(n+1)² = a_n² - 3b_n²

[deadinsoul]

Au fait pour la récurrence, tu as trouvé a_n et b_n, mais dans l'énoncé on te demandait aussi de montrer que "a_n et b_n sont des entiers positifs.". Il faut que tu le montres dans ta récurrence, c'est très rapide à faire ça prend une ou deux lignes, mais il faut le faire.

Sayai je pense avoir fini par répondre à la question 1 entièrement:

Initialisation:

u^1= 2 + V3
v^1= 2 - V3

a_1=2
b_1=1

On a bien a_1 et b_1 2 entiers positifs.

Hérédité:

u^(n+1) = u^n * u^1 = (a_n + b_nV3)(2 + V3)
v^(n+1) = v^n * u^1 = (a_n - b_nV3)(2 - V3)

= 2a_n + a_nV3 + 2b_nV3 + 3b_n
= 2a_n - a_nV3 - 2b_nV3 + 3b_n

= 2a_n + 3b_n +V3(a_n + 2b_n)
= 2a_n + 3b_n -V3(a_n + 2b_n)

= a_(n+1) + b_(n+1)V3
= a_(n+1) - b_(n+1)V3

Conclusion Si u^(n+1)=a_(n+1) + b_(n+1)V3 et v^(n+1)=a_(n+1) - b_(n+1)V3 alors u^n= a_n + b_nV3 et v^n=a_n - b_nV3

Expression de a_(n+1) et b_(n+1) en fonction de a_n et b_n:
a_(n+1)=2a_n + 3b_n
b_(n+1)=a_n + 2b_n

2) a_n*b_(n+1) - a_(n+1)*b_n = a_n² - 3b_n²

et ensuite je ne comprend pas comment vous faites pour voir que c'est aussi égal à a_(n+1)² - 3b_(n+1)² et puis il y a un problème , nous voulions reculer jusqu'a u^0=1 or on commence à u^1=2+V3

[romani01]

Salut.
Comme Primperan,qui t'a bien aidé semble absent ,je t'aide pour cette question.
Tu pars mal pour montrer que et sont des entiers positifs.
Comme te l'as précisé Primperan,il faut deux ou trois lignes.
Initialisation:on a et ,
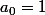n=0 donc et comme et 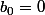(tu les
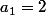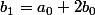as déterminés précédemment) on a et donc 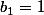.Voilà,pour l'initialisation.
Hérédité:
C'est beaucoup plus simple.
On suppose que donc donc .
Sauf erreur de ma part.