Exercice de Spécialité Maths CONGRUENCES
13 messages
- Page 1 sur 1
Exercice de Spécialité Maths CONGRUENCES
Démontré que pour tout entier naturel n , 7^2n+3 est divisible par 4.
Re: Exercice de Spécialité Maths CONGRUENCES
Bonsoir,
Avez vous envisagé un raisonnement par récurrence ?
Allez je vous donne la phase d'initialisation pour n=0, 7^{2*0}+3=4 qui est effectivement divible par 4
A vous de jouer pour la phase d'héridité
Avez vous envisagé un raisonnement par récurrence ?
Allez je vous donne la phase d'initialisation pour n=0, 7^{2*0}+3=4 qui est effectivement divible par 4
A vous de jouer pour la phase d'héridité
Re: Exercice de Spécialité Maths CONGRUENCES
salut
première méthode :
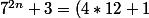^n + 3)
première méthode :
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Exercice de Spécialité Maths CONGRUENCES
Bonsoir , non car je dois utiliser les congruences.
Zygomatique je ne vois pas où vous voulez en venir ?
Zygomatique je ne vois pas où vous voulez en venir ?
Re: Exercice de Spécialité Maths CONGRUENCES
ben avec les congruences c'est trivial avec ce que j'ai écrit ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Exercice de Spécialité Maths CONGRUENCES
Je ne comprends pas votre égalité et ou il faut en venir
Re: Exercice de Spécialité Maths CONGRUENCES
baptc47 a écrit:Je ne comprends pas votre égalité et ou il faut en venir
Que pensez vous d'un nombre qui soit divisible par 4 et dont le reste vaille 1 (en terme de congruence) ?
Re: Exercice de Spécialité Maths CONGRUENCES
Il est congru à 1 modulo 4 oui mais après je ne sais pas
Re: Exercice de Spécialité Maths CONGRUENCES
Du coup sa donne ça :
7^2=-1^2[4]
7^2n=-1^2n[4]
7^2n+3=-1^2n +3[4] ?
7^2=-1^2[4]
7^2n=-1^2n[4]
7^2n+3=-1^2n +3[4] ?
Re: Exercice de Spécialité Maths CONGRUENCES
baptc47 a écrit:Du coup sa donne ça :
7^2=-1^2[4]
7^2n=-1^2n[4]
7^2n+3=-1^2n +3[4] ?
Bonjour,
Souvenez vous que Zygomatique vous avez mâché le travail en réécrivant
et ensuite vous pouvez conclure
Re: Exercice de Spécialité Maths CONGRUENCES
Bjr oui c'est vrai le 1^n devient un 1 du coup sa marche , merci bcp
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
