Exercice recherche fonctions 1ère S

par **Cheche** » 07 Mar 2013, 18:02

Reprenons l'exercice initial :

Donc :

Posons :

- en 0, tu as un maximum local.
- en

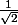
et [tex]- \frac{1}{\sqrt{2}}[tex], tu as deux minimum locaux (qui sont globaux aux passages).

Ok ?

par **BlackiStorm72** » 07 Mar 2013, 18:07

Ok grosse erreur de concentration de ma part je sais pas toi mais moi je trouve que ça correspond!

par **BlackiStorm72** » 07 Mar 2013, 18:15

On fait la question 2?
Question 2:
Soit f la fonction définie sur R par f(x)= x^3+x^2+ax
Quelles sont les valeurs de a pour lesquelles la fonction f est strictement croissante?

par **Cheche** » 07 Mar 2013, 18:17

Je t'écoute.

par **BlackiStorm72** » 07 Mar 2013, 18:21

Bah en fait je n'ai jamais étudier ce genre de fonction du troisième degrés

par **Cheche** » 07 Mar 2013, 18:22

Et la dérivée pour connaître les variations d'une fonction, ça ne te dit rien ?

par **BlackiStorm72** » 07 Mar 2013, 18:25

Si mais après le a on en fait quoi :
f'(x)= 3x^2+2X+a ?

par **BlackiStorm72** » 07 Mar 2013, 18:28

Je suis désolé je dois aller au foot Merci peut etre à demain!

par **Cheche** » 07 Mar 2013, 18:28

- Le signe de f'(x) ?
- Les variations de f ?

Questions hyper classiques.

Exercice recherche fonctions 1ère S

Qui est en ligne