Exercice : Racine cubique et polynôme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Oplya
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2012, 18:54
-
 par Oplya » 04 Nov 2012, 20:19
par Oplya » 04 Nov 2012, 20:19
Bonsoir, je suis en première S et j'ai un exercice sur les polynômes et les racines cubiques. Les poynômes ça va j'ai compris mais par contre les racines cubiques j'ai un peu de mal.
On considère alpha =
 1
1.
Montrer qu'alpha^3 + 3.alpha - 4 = 0Donc ce qui donne
^3 + 3.(\sqrt[3]{sqrt{5}+2} - \sqrt[3]{sqrt{5}-2}) - 4 = 0)
^3)
donne 4 puisqu'alpha au cube "annule" la racine cubique et donc

= 4
Cependant je n'arrive pas à développer ce produit :
) 2a
2a.
Montrer qu'il existe trois réels a, b et c tels que :
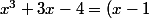(ax^2+bx+c))
(ax^2+bx+c))

+x(c-b)-c)
b.
Déterminer a,b et cD'après l'unicité del'écriture d'u polynôme on obtient par identification le système suivant :

a=1, b=4 c=4 donc
(x^2+4x+4)) c. Montrer qu'alpha est un entier.
c. Montrer qu'alpha est un entier.Là par contre je suis perdu.
Merci d'avance à ceux qui pourront m'apporter un peu d'aide.
-
christ74
- Membre Naturel
- Messages: 35
- Enregistré le: 29 Déc 2010, 16:58
-
 par christ74 » 04 Nov 2012, 21:20
par christ74 » 04 Nov 2012, 21:20
Oplya a écrit:On considère alpha =
 1
1.
Montrer qu'alpha^3 + 3.alpha - 4 = 0Donc ce qui donne
^3 + 3.(\sqrt[3]{sqrt{5}+2} - \sqrt[3]{sqrt{5}-2}) - 4 = 0)
^3)
donne 4 puisqu'alpha au cube "annule" la racine cubique et donc

= 4
Cependant je n'arrive pas à développer ce produit :
)
Bonsoir, c'est vrai que
^3 = x)
mais cela n'est pas applicable ici car on a une différence dans les
parentheses.. Tu développes en utilisant l'identité remarquable (a-b)³ = (a-b)(a² - 2ab + b²)= a³ - 3a²b + 3ab² - b³
En ce qui concerne le développement de 3.alpha développe normalement k(a-b) = ka - kb
-
Anonyme
 par Anonyme » 04 Nov 2012, 22:11
par Anonyme » 04 Nov 2012, 22:11
@Oplya
^3=192\sqrt 3)
-
Anonyme
 par Anonyme » 04 Nov 2012, 22:16
par Anonyme » 04 Nov 2012, 22:16
@Oplya
^3 \sim 1)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 04 Nov 2012, 23:13
par Lostounet » 04 Nov 2012, 23:13
christ74 a écrit:Bonsoir, c'est vrai que
^3 = x)
mais cela n'est pas applicable ici car on a une différence dans les
parentheses.. Tu développes en utilisant l'identité remarquable (a-b)³ = (a-b)(a² - 2ab + b²)= a³ - 3a²b + 3ab² - b³
En ce qui concerne le développement de 3.alpha développe normalement k(a-b) = ka - kb

Proud
En ce qui concerne le 3:
* Tu as (presque) montré que: alpha^3 + 3.alpha - 4 = 0
* Tu as montré que pour tout nombre x, on a: x^3 + 3x - 4 = (x - 1)(x^2 + 4x + 4)
* Si tu as que x^3 + 3x - 4 est nul pour un réel x, alors forcément (x - 1)(x^2 + 4x + 4) = 0
Alors: x - 1 = 0
Ou
x^2 + 4x + 4 = 0
x ne peut alors valoir que 1 ou -2 si x^3 + 3x - 4 = 0
* Que vaut donc alpha? Un petit encadrement devrait permettre de conclure.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Anonyme
 par Anonyme » 05 Nov 2012, 13:34
par Anonyme » 05 Nov 2012, 13:34
@Oplya
Attention , il y a peut être une erreur de frappe quelque part ?
car on a
(x^2+4x+4))
-
Oplya
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2012, 18:54
-
 par Oplya » 05 Nov 2012, 14:55
par Oplya » 05 Nov 2012, 14:55
Non il n'y pas d'erreur c'est bien
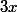
. C'est ce que j'ai dans mon énoncé.
Lostounet merci pour le petit 3 c'est plus clair maintenant, sinon christ74 ta formule m'a bien aidé mais j'ai vraiment du mal avec le développement :
(a-b)³ = (a-b)(a² - 2ab + b²)= a³ - 3a²b + 3ab² - b³ et les racines cubiques me gênait alors j'ai suivi cette propriété :
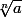
=

donc

=

^{1/3})^3 - [3.(sqrt{5} + 2)^{1/3})^2.(sqrt{5} - 2)^{1/3})] + [3.(sqrt{5} + 2)^{1/3}).((sqrt{5} - 2)^{1/3})^{2}] - (sqrt{5}-2)^{1/3})^3)
 - [(3sqrt{5}+6)^{2/3}.(sqrt{5} - 2)^{1/3})] +[(3sqrt{5}+6)^{1/3}.(sqrt{5} - 2)^{2/3})] - (sqrt{5}-2))
A partir de là je suis bloqué... Mais je me demande surtout si mon raisonnement est correcte. Sinon je me suis dis que un produit est nul si est seulement si un de ses facteurs est nul alors (a-b)(a² - 2ab + b²) = 0.
]=0)

-
Anonyme
 par Anonyme » 05 Nov 2012, 20:09
par Anonyme » 05 Nov 2012, 20:09
@Oplya
OK tu as DONC fait une erreur dans ton raisonnement car
(x^2+4x+4)) ps)
ps) pour développer
^3 + 3(\sqrt[3]{sqrt{5}+2} - \sqrt[3]{sqrt{5}-2}) - 4)
c'est plus facile (à mon avis) de poser :

et

ON cherche donc à montrer que (a- b})^3 + 3(a - b) - 4 = 0
c'est à dire a³ - 3a²b + 3ab² - b³ +3(a-b) - 4 =0
1) On a
^3=\sqrt{5}+2)
et
^3 = \sqrt{5}-2)
et donc a³ - b³ = 4
2) pour développer -3a²b+3ab²
comme -3a²b+3ab²=3ab(b-a)
et comme
 \times sqrt{5}-2)}=1)
on a donc -3a²b+3ab²=3(b-a)
et donc on a bien le résultat demandé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 111 invités
