Bonjour
Moi ce que je ferais (attention je parle de moi et non de vous ce que vous devriez faire)
et en plus c'est pas certain que le prof l'acceptera si vous faite ça
mais comme personne n'est venu je poste mais vous pourriez me dire comment je les sort de mon chapeau les deux scalaires t et u
bah en fait tout se démontre mais c'est un peu long
d'autant plus que j'ai choisi de m'emmerder car il y a certainement plus simple
mais comme j'ai vu que la puissance d'un point par rapport à un cercle n'est pas utile ici (en tout cas j'en ai l'impression) alors je me suis dit
bah autant s'emmerder à fond (mais je ne vous conseille pas de vous emmerder donc attendez quelqu'un de plus compétent)
pour la question b)
il s'agit de constater que

est constant
pour la question c)
dans un premier temps on va écrire ces deux points

et

On sait que la construction donnée dans la question a) doit être telle que

et

sont distincts
Comme

est à l'extérieur du cercle on sait donc que l'un de ces deux points

ou

est le plus proche de

et on sait que les mesures géométriques
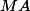
et

ne sont pas nulles
en effet le moint

est à l'extérieur du cercle
Avant d'écrire ces deux points on va poser les deux scalaires
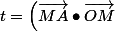.\sqrt {\frac {R^2-OM^2}{MA^2.\left(\vec{MA}\bullet \vec{OM}\right)^2}+\frac {1}{MA^4}}-\dfrac {\vec{MA}\bullet \vec{OM}}{MA^2})
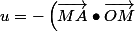.\sqrt {\frac {R^2-OM^2}{MA^2.\left(\vec{MA}\bullet \vec{OM}\right)^2}+\frac {1}{MA^4}}-\dfrac {\vec{MA}\bullet \vec{OM}}{MA^2})
Si

est le point le plus proche de

alors
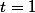
et alors

et

Si

est le point le plus éloigné de

alors
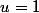
et alors

et

À partir de là on a nos deux points et on devra vérifier ce qui est demandé tantôt en prennant

et

tantôt en prenant

et

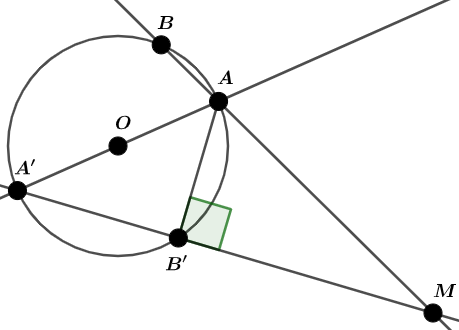
par ailleurs on peut remarquer (et démontrer) l'angle droit de la figure en posant le point
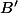
les reste est facile car on sait écrire tous les points (même les points
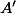
et
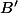
)