Exercice prise d'initiative dérivation

[serine]

bonjour

voila j'ai un gros problème, je voulais m'entraîner à résoudre des exercices à prise d'initiative suite à un conseil du proff, mais je n'y arrive pas, j'ai toujours le même problème: commencer. :mur: :mur:

est ce que quelqu'un peut m'aider svp.

merci pour tout. voila mon exercice:

on considère la fonction carré et sa courbe représentative Cf tracée dans un repère.
Existe-t-il un point A de Cf tel que la tangente à Cf en A soit parallèle à la droite d'équation y=x ?
:help: :help:

[SaintAmand]

Bonjour,

on considère la fonction carré et sa courbe représentative Cf tracée dans un repère.
Existe-t-il un point A de Cf tel que la tangente à Cf en A soit parallèle à la droite d'équation y=x ?

Ça un exercice à prise d'initiative ? Je ne le trouve pas particulièrement motivant, la réponse est immédiate, et on ne peut pas dire que le problème soit riche.

Deux droites parallèles sont deux droites de même direction. La direction d'une droite est donnée par son coefficient directeur (quand il existe). Quel est le coefficient directeur de la tangente au point d'abscisse x de la courbe Cf ?

[Dinozzo13]

Salut !

est la courbe représentative de la fonction .
Soit le point d'abscisse réelle appartenant à .
Si alors a pour coordonnées .
Détermine de façon générale, une équation de la tangente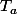 à au point d'abscisse réelle .
Ensuite, sert du fait que la tangente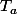 est parallèle à la droite d'équation 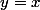si et seulement si ces deux droites ont même coefficient directeur :++:

[serine]

bonsoir
le coef directeur est 1.

puisque la dérivée de f(x)=x² est f'(x)=2x

[Lostounet]

Salut,
Je ne comprends pas?

Quelle est la forme d'une équation d'une tangente à une courbe en un point d'abscisse a?

[Dinozzo13]

Salut,
Je ne comprends pas?

Quelle est la forme d'une équation d'une tangente à une courbe en un point d'abscisse a?

Hey ! Slt Lostounet !

Une équation de la tangente à la courbe représentative au point d'abscisse est :

[serine]

je devrais donc utiliser les coordonnée de A pour calculer l'équation de la tangente?
donc l'équation serait
y= f'(a)(x-a)+f(a) ?

[serine]

je devrais donc utiliser les coordonnée de A pour calculer l'équation de la tangente?
donc l'équation serait
y= f'(a)(x-a)+f(a) ?

et est ce que je remplace a par le coef directeur qui est = 1?

[Lostounet]

Hey ! Slt Lostounet !

Une équation de la tangente à la courbe représentative au point d'abscisse est :

Haha Salut biscuit
Et je le sais bien (on a fait le chapitre), je posais la question à Serine :ptdr:

et est ce que je remplace a par le coef directeur qui est = 1?

Oui, exactement !

f'(a) = 1

[serine]

ok je vais ça

merci pour tout ;)

[serine]

bonsoir,
l'equation est donc: y =- 1(x - 1) +1
y = -x + 2

c'est bien sa? :/
ah oui et une question svp: comment calculer f'(x)=1 :hein:


merci