Exercice de première S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 14:01
par just.lala » 09 Oct 2014, 14:01
Bonjour, après avoir passé un semaine dessus, cet exercice m'énerve, c'est pour ça que j'ai besoin d'aide !
A tout point M du segment [AB], on associe les triangles équilatéraux AMP et MBQ.
1. Déterminer la position du point M pour que l'aire du triangle MPQ soit maximale.
2. Déterminer la position du point M pour que l'aire du quadrilatère ABQP soit minimale.
(On pourra choisir x= distance AM et prendre AB=1 unité de longueur)
Merci d'avance
JUJU !
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 09 Oct 2014, 14:16
par Shew » 09 Oct 2014, 14:16
just.lala a écrit:Bonjour, après avoir passé un semaine dessus, cet exercice m'énerve, c'est pour ça que j'ai besoin d'aide !
A tout point M du segment [AB], on associe les triangles équilatéraux AMP et MBQ.
1. Déterminer la position du point M pour que l'aire du triangle MPQ soit maximale.
2. Déterminer la position du point M pour que l'aire du quadrilatère ABQP soit minimale.
(On pourra choisir x= distance AM et prendre AB=1 unité de longueur)
Merci d'avance
JUJU !
Ok on part de AB = 1 donc on pose
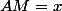
et
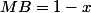
comme les triangles AMP et MBQ sont equilateraux donc les côtés ont même mesure . On cherche la hauteur h de chacun des triangles en utilisant pythagore .
-
mathelot
 par mathelot » 09 Oct 2014, 14:18
par mathelot » 09 Oct 2014, 14:18
bonjour,
faut faire le lien entre deux formules
- Aire d'un triangle = (base

hauteur) /2
- côté du triangle équilatéral égal à

(ou à
)
)
donc calculer la hauteur du triangle , fonction de

-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Oct 2014, 14:32
par Monsieur23 » 09 Oct 2014, 14:32
just.lala a écrit:Bonjour, après avoir passé un semaine dessus, cet exercice m'énerve, c'est pour ça que j'ai besoin d'aide !
A tout point M du segment [AB], on associe les triangles équilatéraux AMP et MBQ.
1. Déterminer la position du point M pour que l'aire du triangle MPQ soit maximale.
2. Déterminer la position du point M pour que l'aire du quadrilatère ABQP soit minimale.
(On pourra choisir x= distance AM et prendre AB=1 unité de longueur)
Merci d'avance
JUJU !
On note tout de même qu'il est marqué, avant "Sujet" qu'il ne faut mettre ni "Urgent", ni "DM pour demain". Bien joué, tu as mis les deux. :ptdr:
« Je ne suis pas un numéro, je suis un homme libre ! »
-
mathelot
 par mathelot » 09 Oct 2014, 14:41
par mathelot » 09 Oct 2014, 14:41
tu as la possibilité de changer le titre ?
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 14:47
par just.lala » 09 Oct 2014, 14:47
Mais je ne suis pas censée trouver une équation trinôme du 2nd degrés ?
Et je dois trouver la hauteur du triangle AMP ?
-
mathelot
 par mathelot » 09 Oct 2014, 14:48
par mathelot » 09 Oct 2014, 14:48
ok, calcule la hauteur du triangle équilatéral en fonction de la longueur du côté (via Pythagore),
-
mathelot
 par mathelot » 09 Oct 2014, 14:49
par mathelot » 09 Oct 2014, 14:49
just.lala a écrit:Mais je ne suis pas censée trouver une équation trinôme du 2nd degrés ?
Et je dois trouver la hauteur du triangle AMP ?
oui
::::::::
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 09 Oct 2014, 14:50
par Shew » 09 Oct 2014, 14:50
just.lala a écrit:Mais je ne suis pas censée trouver une équation trinôme du 2nd degrés ?
Et je dois trouver la hauteur du triangle AMP ?
Trouvez les hauteurs des deux triangles equilateraux pour exprimer l'aire de chacun des triangles en fonction d'elle (la hauteur) .
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 15:00
par just.lala » 09 Oct 2014, 15:00
J'ai appelé H le milieu de [AM] et R le milieu de [MB]
PH²=(3x²)/4 et QR²= (5x²+10x+3)/4
C'est bien ça ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 09 Oct 2014, 15:03
par Shew » 09 Oct 2014, 15:03
just.lala a écrit:J'ai appelé H le milieu de [AM] et R le milieu de [MB]
PH²=(3x²)/4 et QR²= (5x²+10x+3)/4
C'est bien ça ?
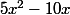
mais pour 3 je ne vois pas ... . Je pense plutot qu'il s'agit de
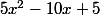
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 15:07
par just.lala » 09 Oct 2014, 15:07
Voici mon calcul :
QR²= (1-x)²- ((1-x)/2)
= 1=2x+x² - (1+2x+²)/4
= (4+8x+4x²-1+2x+x²)/4
= (5x²+10x+3)/4
-
mathelot
 par mathelot » 09 Oct 2014, 15:11
par mathelot » 09 Oct 2014, 15:11
par exemple
=\sqrt{3}=\frac{2h}{x})
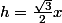
ou par Pythagore
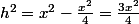
du coup, pour l'autre triangle de hauteur h'
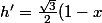)
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 09 Oct 2014, 15:16
par Shew » 09 Oct 2014, 15:16
just.lala a écrit:Voici mon calcul :
QR²= (1-x)²- ((1-x)/2)
= 1=2x+x² - (1+2x+²)/4
= (4+8x+4x²-1+2x+x²)/4
= (5x²+10x+3)/4
En effet je me suis trompé aussi avec le signe enfait il s'agit plutot de :
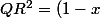^2 - \left(\frac{(1 - x)}{2}\right)^2 = (1 - x)^2 - \frac{(1 - x)^2}{4} = \frac{4(1 - x)^2 - (1 - x)^2}{4} = \frac{3(x - 1)^2}{4})
. Le developpement ici ne sert à rien car nous supprimons l'elevation au carré on a donc après simplification :
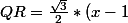)
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 15:19
par just.lala » 09 Oct 2014, 15:19
D'accord merci par ccontre la je men vas pour une heure, je reviens. Encore merci, Juju !

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Oct 2014, 16:57
par chan79 » 09 Oct 2014, 16:57
On peut prendre MQ, comme base de MPQ.
La hauteur correspondante est égale aux hauteurs de ABP.
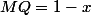
hauteur =
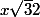
L'aire de MPQ sera maximale si x(1-x) l'est.
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 17:07
par just.lala » 09 Oct 2014, 17:07
Pourquoi x(1-x) ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Oct 2014, 18:37
par chan79 » 09 Oct 2014, 18:37
just.lala a écrit:Pourquoi x(1-x) ?
l'aire de MPQ est
\times x\fra{\sqr{3}}{2})
elle est maxi si
x)
est maxi
-
just.lala
- Messages: 7
- Enregistré le: 09 Oct 2014, 13:50
-
 par just.lala » 09 Oct 2014, 19:15
par just.lala » 09 Oct 2014, 19:15
J'ai calculé les aires de MQB et de APM ça a servi à quelque chose ?
Parce que je ne vois comment tu as fait pour arriver à ce résultat.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Oct 2014, 19:40
par chan79 » 09 Oct 2014, 19:40
Regarde ce dessin

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 117 invités

