EXERCICE PREMIÈRE SM EQUATIONS SECOND DEGRE

[james7kidd777]

Bonjour s'il vous plait je voudrai la réponse à la question 3).
A la question 2 j'ai trouvé :

On considère l'équation (E): avec
1) Montrer que (E) est équivalent à une équation de second degré que l'on précisera.
2)Résoudre cette équation d'inconnu a.
3) En déduire les solutions de (E).
Merci déjà en avance pour vos réponses.

[infernaleur]

Salut regarde ce que donne a + x avec le résultat de Ta question précédente sa t'enlevera une racine

[james7kidd777]

Oui ça enlève une racine et je trouve .
et avec ça . ce qui ne vérifie pas l'équation.

[Lostounet]

Salut,
Élever au carré une équation introduit des solutions parasites.

N'oublie pas aussi que, racine((x+1))^2 vaut x+1 si x>=-1 ou bien -x-1 si x<-1.
Du coup tu as aussi autre chose à dire.

Mais en conclusion effectivement il me semble que (E) n'admet aucune racine réelle.

[james7kidd777]

Pourtant quand j'utilise une calculatrice pour résoudre en fixant
Il y'a une solution qui vérifie bien l'équation :
vraiment bizarre cette équation !!!
ça m'a déjà pris toute une journée. ouf

[Lostounet]

Oui mais si a=2, et que x=2 marche pour (E) n'oublie pas que
a=x^2+x+1.

Cela signifie que a=2 et x=2 ne peut pas réaliser la première condition..
En fait (E) et a=x^2+x+1 forment un système d'équations à deux inconnues a et x.

Tu montres que si a=x^2+x+1 et (E) est vraie il n'y a pas de solution. Il faut aussi tenir compte de ce que je t'avais dit tu n'as pas traité les deux cas.

Mais je ne sais pas si ton énoncé est juste... tu ne nous dit pas si le a est le même dans les deux questions.

[Ben314]

Salut,

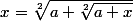
On considère l'équation (E): avec
1) Montrer que (E) est équivalent à une équation de second degré que l'on précisera.
2)Résoudre cette équation d'inconnu a.

Le problème, c'est que l'exercice utilise des notations "non habituelles" : dans la question 2) de l'énoncé on te précise qu'il faut résoudre cette équation "d'inconnue a", c'est à dire en considérant que x est "connu" (i.e. que c'est un paramètre) et en cherchant la valeur de a (en fonction de x bien sûr).
D'habitude, au niveau des lettres "a" et "x" c'est plutôt le contraire qu'on utilise : "a" est un paramètre (connu) et "x" est la "variable" (à calculer en fonction de a). Donc ça déroute un peu.
Sans parler du fait que dans la question 1), on aurais déjà du préciser qui est le paramètre et qui est la variable vu que l'équation en question, elle est du second degré si c'est "a" la variable, mais elle n'est pas du second degré si c'est "x" la variable (il y a du x^3).

Pourtant quand j'utilise une calculatrice pour résoudre en fixant

Et là, ton truc de chercher la valeur de x lorsque a=1, ça ne colle pas avec la logique de l'exercice qui lui procède dans l'autre sens : C'est "x" qui est sensé être "connu" et c'est "a" qu'on cherche.

[Tiruxa47]

Bonjour,

En effet l'énoncé est surprenant..

Comme l'a dit Lostounet, il faut prendre des précautions pour conserver l'équivalence lors des élévations au carré.
En général on pose ces conditions pour x, mais là c'est pour a.

Lors de la deuxième élévation au carré, la condition posée est x²-a positif, c'est à dire a inférieur à x².

Cela veut dire que les solutions doivent vérifier cette inégalité.
C'est une équation du second degré, son delta est strictement positif donc elle admet 2 solutions
La solution que tu as trouvée et une autre (à trouver...)
Or x²+x+1 ne vérifie pas la condition (être inférieur à x²) car x²+x+1 > x² puisque x est positif (x doit être égal à une racine carréedans (E))

Par contre la deuxième solution vérifie la condition et donc convient

Pour la 3) il suffit de résoudre l'équation en x obtenue à la deux, j'ai trouvé x=(1+racine(1+4a))/2
qui donne bien x=2 lorsque a=2