Bonjour,
J'ai un devoir à rendre et je bloque sur cet exercice,merci d'avance de m'aidée
1-Restitution Organisée de Connaissances
Soit f la fonction définie sur [-4;+inf[ par f(x)=racine de x+4
En vous inspirant du cours,démontrer que la fonction f est croissante sur son ensemble de définition(question répondue)
2-Sur votre calculatrice,tracer la courbe représentant f et la droite d'équation y=x-2.Proposer une fenêtre d'affichage montrant bien le point d'intersection des 2 courbes.On note A ce point(J'ai réussi à tracer les courbes,mais je ne comprends ce qu'ils veulent dire par fenêtre d'affichage).
3-Dans cette question,on cherche à déterminer l'abscisse du point A par le calcul.
a-Montrer que,si x est l'abscisse du point A,alors x-2 est plus grand que 0.
b-Montrer que x vérifie l'équation x au carré-5x=0
c-Conclure.
Voilà mon exercice et encore merci pour ceux qui m'aideront.
Exercice de maths
5 messages
- Page 1 sur 1
Re: exercice de maths
Proposer une fenêtre d'affichage montrant bien le point d'intersection des 2 courbes.
C'est le choix d'amplitude de la fenêtre d'affichage par exemple
a-Montrer que,si x est l'abscisse du point A,alors x-2 est plus grand que 0.
Sur
b-Montrer que x vérifie l'équation x au carré-5x=0
Donc ...
Re: exercice de maths
Bonjour;
1)
Soient\in[-4;+\infty[^2) avec
avec 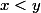 .
.
-f(x)}{y-x} = \dfrac{\sqrt{y+4}-\sqrt{x+4}}{y-x} =\dfrac{(\sqrt{y+4}-\sqrt{x+4})(\sqrt{y+4}+\sqrt{x+4})}{(y-x)(\sqrt{y+4}+\sqrt{x+4})})
(\sqrt{y+4}+\sqrt{x+4})}=\dfrac{y+4-x-4}{(y-x)(\sqrt{y+4}+\sqrt{x+4})}=\dfrac{y-x}{(y-x)(\sqrt{y+4}+\sqrt{x+4})}=\dfrac{1}{\sqrt{y+4}+\sqrt{x+4}}>0) ;
;
donc est strictement croissante .
est strictement croissante .

Pour le reste , Carpate t'as donné assez d'indices pour finir ton exercice .
1)
Soient
donc

Pour le reste , Carpate t'as donné assez d'indices pour finir ton exercice .
Re: exercice de maths
Salut,
Pour tout , on a
, on a  épicétout
épicétout
Où la première équivalence provient du fait (vu au collège) que deux nombre positifs sont dans le même ordre que leur carré.
Et c'est totalement idiot d'aller s’emmerder avec un calcul de pente dans le cas d'une fonction aussi bénigne où la variable n’apparaît qu'une seule fois.
n’apparaît qu'une seule fois.
Et, à mon sens, c'est caricatural de la façon dont on enseigne ces dernier temps : ne surtout pas réfléchir et appliquer le plus bêtement possible et sans tenir compte du contexte des "recettes toutes faites" : On m'a dit que pour couper du bois il fallait une tronçonneuse, ben pour couper une allumette, vu que c'est du bois, je prend la tronçonneuse. . .
Pour tout
Où la première équivalence provient du fait (vu au collège) que deux nombre positifs sont dans le même ordre que leur carré.
Et c'est totalement idiot d'aller s’emmerder avec un calcul de pente dans le cas d'une fonction aussi bénigne où la variable
Et, à mon sens, c'est caricatural de la façon dont on enseigne ces dernier temps : ne surtout pas réfléchir et appliquer le plus bêtement possible et sans tenir compte du contexte des "recettes toutes faites" : On m'a dit que pour couper du bois il fallait une tronçonneuse, ben pour couper une allumette, vu que c'est du bois, je prend la tronçonneuse. . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: exercice de maths
Variante (et sans tronçonneuse !) :
 = x+4<br />\end{array})
 = \sqrt{x}<br />\end{array})
 = \sqrt{x+4}<br />\end{array})
Les 2 fonctions g et h étant croissantes,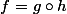 est croissante sur
est croissante sur 
Les 2 fonctions g et h étant croissantes,
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
