Exercice de maths sur la dérivation
34 messages
- Page 1 sur 2 - 1, 2
 Exercice de maths sur la dérivation
Exercice de maths sur la dérivation
Bonjour à tous.
Je suis un élève de 1ère S et on m'a donc donné un devoir pour ces vacances mais que je n'arrive pas vraiment à faire... J'aimerais si possible qu'on me donne alors un petit coup de main s'il vous plaît. J'ai réussi à faire la première question, où je trouve comme résultat f'(x)= -ax²-2xb+a/ (x²+1)². Il me reste donc les autres questions à faire.
Voici l'énoncé : https://image.noelshack.com/fichiers/20 ... maths.jpeg
Je suis un élève de 1ère S et on m'a donc donné un devoir pour ces vacances mais que je n'arrive pas vraiment à faire... J'aimerais si possible qu'on me donne alors un petit coup de main s'il vous plaît. J'ai réussi à faire la première question, où je trouve comme résultat f'(x)= -ax²-2xb+a/ (x²+1)². Il me reste donc les autres questions à faire.
Voici l'énoncé : https://image.noelshack.com/fichiers/20 ... maths.jpeg
Re: Exercice de maths sur la dérivation
Mondor a écrit: f'(x)=( -ax²-2xb+a)/ (x²+1)².
attention, tu dois parenthéser le numérateur
Modifié en dernier par mathelot le 01 Mar 2019, 16:13, modifié 1 fois.
Re: Exercice de maths sur la dérivation
Bjr
Ta dérivée serait bonne si il y avait des parenthèses au bon endroit.
Pour le reste rien de bien compliqué.
2 ) En effet tu traduis les hypothèses:
Pour le point A f(0)=2 ---> b=2.
Pour les tangentes // : f'(1)=f'(0) ---->a=-1
On retrouve bien l'expression de f donnée dans l'énoncé.
Ta dérivée serait bonne si il y avait des parenthèses au bon endroit.
Pour le reste rien de bien compliqué.
2 ) En effet tu traduis les hypothèses:
Pour le point A f(0)=2 ---> b=2.
Pour les tangentes // : f'(1)=f'(0) ---->a=-1
On retrouve bien l'expression de f donnée dans l'énoncé.
Re: Exercice de maths sur la dérivation
pour la (3)
=\dfrac{x^2-4x-1}{(x^2+1)^2})
factorise le numérateur de la dérivée, pour faire ensuite:
-le tableau de signes de la dérivée
- le tableau des variations de f (avec calcul des limites aux bornes du domaine)
factorise le numérateur de la dérivée, pour faire ensuite:
-le tableau de signes de la dérivée
- le tableau des variations de f (avec calcul des limites aux bornes du domaine)
Modifié en dernier par mathelot le 01 Mar 2019, 16:32, modifié 2 fois.
Re: Exercice de maths sur la dérivation
Question (4):
Quel est le coefficient directeur d'une tangente horizontale ?
Question (5)
Calcule les coordonnées des points E et F, puis le coefficient directeur de la droite (EF)
Pour montrer que (EF) est tangente à la courbe (C) en F, il s'agit de vérifier une égalité.Laquelle ?
Quel est le coefficient directeur d'une tangente horizontale ?
Question (5)
Calcule les coordonnées des points E et F, puis le coefficient directeur de la droite (EF)
Pour montrer que (EF) est tangente à la courbe (C) en F, il s'agit de vérifier une égalité.Laquelle ?
Re: Exercice de maths sur la dérivation
Bravo pour être arrivé à cette page !!
comme récompense, je t'offre une place au cinéma, ci-dessous:
https://www.youtube.com/watch?v=2GwSUDm_Rg8
comme récompense, je t'offre une place au cinéma, ci-dessous:
https://www.youtube.com/watch?v=2GwSUDm_Rg8
Re: Exercice de maths sur la dérivation
mathelot a écrit:Mondor a écrit: f'(x)=( -ax²-2xb+a)/ (x²+1)².
attention, tu dois parenthéser le numérateur
Oui effectivement j'ai oublié d'insérer les parenthèses, vous avez raison
Re: Exercice de maths sur la dérivation
aviateur a écrit:Bjr
Ta dérivée serait bonne si il y avait des parenthèses au bon endroit.
Pour le reste rien de bien compliqué.
2 ) En effet tu traduis les hypothèses:
Pour le point A f(0)=2 ---> b=2.
Pour les tangentes // : f'(1)=f'(0) ---->a=-1
On retrouve bien l'expression de f donnée dans l'énoncé.
Merci beaucoup, mais en fait je ne comprends pas pourquoi du coup c'est b=2 puisque il s'agit du point A. Et aussi également comment trouve-t-on le -1 pour a ?
Re: Exercice de maths sur la dérivation
mathelot a écrit:Question (4):
Quel est le coefficient directeur d'une tangente horizontale ?
Question (5)
Calcule les coordonnées des points E et F, puis le coefficient directeur de la droite (EF)
Pour montrer que (EF) est tangente à la courbe (C) en F, il s'agit de vérifier une égalité.Laquelle ?
Pour la question 4, le coefficient directeur d'une tangente horizontale est (yB−yA)/ (xB−xA)
Au niveau de la question 5, est-ce que il s'agirait de l'égalité : Ta:y= f'(a) (x-a)+f(a) ? Il s'agit de l'équation réduite d'une tangente.
Re: Exercice de maths sur la dérivation
Bonjour,
pour la 1)=-\frac{ax^2+2bx-a}{(x^2+1)^2}) , pour la 2) les informations fournies par l'énoncé traduisent les égalités
, pour la 2) les informations fournies par l'énoncé traduisent les égalités =2) et
et =f'(0)) , donc
, donc  et
et  vérifient un système à résoudre. Pour la 3), il suffit d'étudier le signe de la dérivée, pour la 4), une tangente horizontale au point d'abscisse
vérifient un système à résoudre. Pour la 3), il suffit d'étudier le signe de la dérivée, pour la 4), une tangente horizontale au point d'abscisse  se caractérise par
se caractérise par =0) , reste à savoir si cette équation admet des solutions. Pour la 5), tu connais l'expression de la tangente à un point d'abscisse
, reste à savoir si cette équation admet des solutions. Pour la 5), tu connais l'expression de la tangente à un point d'abscisse  :
: 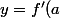(x-a)+f(a)) , il te suffit de montrer que la droite
, il te suffit de montrer que la droite ) coïncide avec la tangente en
coïncide avec la tangente en  en un point et qu'elles ont le même coefficient directeur.
en un point et qu'elles ont le même coefficient directeur.
pour la 1)
Re: Exercice de maths sur la dérivation
je factorise la dérivée
^2-4-1=(x-2)^2-\sqrt{5}^2=(x-2-\sqrt{5})(x-2+\sqrt{5}))
la dérivée s'annule en changeant de signe pour les valeurs
 et
et 
la dérivée s'annule en changeant de signe pour les valeurs
Re: Exercice de maths sur la dérivation
Mondor a écrit:Il y aurait quelqu'un pour m'aider s'il vous plaît ??
où en es tu?
Re: Exercice de maths sur la dérivation
Mondor a écrit:aviateur a écrit:Bjr
Ta dérivée serait bonne si il y avait des parenthèses au bon endroit.
Pour le reste rien de bien compliqué.
2 ) En effet tu traduis les hypothèses:
Pour le point A f(0)=2 ---> b=2.
Pour les tangentes // : f'(1)=f'(0) ---->a=-1
On retrouve bien l'expression de f donnée dans l'énoncé.
Merci beaucoup, mais en fait je ne comprends pas pourquoi du coup c'est b=2 puisque il s'agit du point A. Et aussi également comment trouve-t-on le -1 pour a ?
Les coordonnées de A sont (0;2). A appartient à la courbe Cf. Donc f(0)=2. Remplace x par 0 dans l'expression de f(x),pour commencer le calcul de b.
Re: Exercice de maths sur la dérivation
mathelot a écrit:Mondor a écrit:aviateur a écrit:Bjr
Ta dérivée serait bonne si il y avait des parenthèses au bon endroit.
Pour le reste rien de bien compliqué.
2 ) En effet tu traduis les hypothèses:
Pour le point A f(0)=2 ---> b=2.
Pour les tangentes // : f'(1)=f'(0) ---->a=-1
On retrouve bien l'expression de f donnée dans l'énoncé.
Merci beaucoup, mais en fait je ne comprends pas pourquoi du coup c'est b=2 puisque il s'agit du point A. Et aussi également comment trouve-t-on le -1 pour a ?
Les coordonnées de A sont (0;2). A appartient à la courbe Cf. Donc f(0)=2. Remplace x par 0 dans l'expression de f(x),pour commencer le calcul de b.
En fait je suis encore à la question 2 car c'est elle qui me bloque. Oui effectivement f(0)=2, ça j'ai bien compris.Mais du coup quand on remplace x par 0 dans f'(x) ça nous donne :
f'(x)= (-ax²-2xb+a)/ (x²+1)²
f'(0)= a/1
Et quand je trouve ça, je ne vois pas en quoi ceci peut m'aider en fait
Re: Exercice de maths sur la dérivation
Tuvasbien a écrit:Bonjour,
pour la 1), pour la 2) les informations fournies par l'énoncé traduisent les égalités
et
, donc
et
vérifient un système à résoudre. Pour la 3), il suffit d'étudier le signe de la dérivée, pour la 4), une tangente horizontale au point d'abscisse
se caractérise par
, reste à savoir si cette équation admet des solutions. Pour la 5), tu connais l'expression de la tangente à un point d'abscisse
:
, il te suffit de montrer que la droite
coïncide avec la tangente en
en un point et qu'elles ont le même coefficient directeur.
Il s'agit donc de faire une égalité avec f'(0)= f'(1) en remplaçant bien évidemment les x, et ensuite on va trouver des valeurs avec des a et des b. Et quand on aura ça il faudra faire un système?
Re: Exercice de maths sur la dérivation
Les égalités f'(0)=f'(1) et f(0)=2 forment un système d'inconnue (a,b)
Re: Exercice de maths sur la dérivation
Mondor a écrit:Pour le point A f(0)=2 ---> b=2.
En fait je suis encore à la question 2 car c'est elle qui me bloque. Oui effectivement f(0)=2, ça j'ai bien compris.Mais du coup quand on remplace x par 0 dans f'(x) ça nous donne :
f'(x)= (-ax²-2xb+a)/ (x²+1)²
f'(0)= a/1
Et quand je trouve ça, je ne vois pas en quoi ceci peut m'aider en fait[/quote]
C est dans f et non pas f' qu il faut remplacer x par zero
Re: Exercice de maths sur la dérivation
Oh non au final je viens de trouver en utilisant la formule f(x). En remplaçant x par 0
f(x) = (ax+b)/(x²+1)=2
Donc f(0)= a*0+b/0²+1=2
b/1=2
Donc b=2
f(x) = (ax+b)/(x²+1)=2
Donc f(0)= a*0+b/0²+1=2
b/1=2
Donc b=2
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
