Exercice de Maths Polynômes

[tribys]

Bonjour je suis sur un exercice que je n'arrive pas accomplir l'exercice est le suivant

Exercice 8

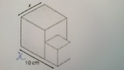
Les deux cubes sont tels que la somme des mesures de leur côtés est égale à 10 cm. On note x la mesure du côté de l'un d'entre eux.
Exercice de Maths Polynômes
Déterminer la valeur de x pour laquelle la somme des volumes des deux cubes est minimale.

Mes recherches:

j'ai d'abord écrit la forme f(x)= X^3+(10-x)^3
J'ai pensé qu'il faut trouver l'extremum donc en trouvant la forme canonique on peut trouver le sommet donc j'ai simplifié
Cela donne 200-220x+30x^2-x^3.
Mais ensuite avec ces x au cube je n'ai pas réussi a mettre sous forme canonique.
Si quelqu'un pourrait m'aider et m'explique ça serait sympa merci d'avance.

[zygomatique]

salut

et si tu faisais une étude cette fonction ?

dérivée, signe de la dérivée, variation, extremum éventuel .... ou reconnaître un type particulier de fonction ....

et ton développement est faux ....

[tototo]

Bonjour

min x^3+(10-x)^3=f(x)

f'(x)=3*x^2+3*-1*(10-x)^2=3x^2-3(10-x)^2

On veut x1 tel que f'(x1)=0 et f"(x1)>0