Exercice math olympiade
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Avr 2013, 17:40
par Ericovitchi » 18 Avr 2013, 17:40
Moi j'essayerai par récurrence. C'est vrai pour n=1, suppose la relation vraie pour n et montre que c'est encore vrai pour n+1.
l'astuce sera d'écrire que
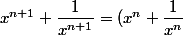(x+\dfrac{1}{x})-(x^{n-1}+\dfrac{1}{x^{n-1}}))
Et puis aussi que 4 cos(na) cos (a) - 2 cos((n-1)a) = 2cos((n+1)a) et on arrive au bout
-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 18 Avr 2013, 21:32
par hammana » 18 Avr 2013, 21:32
Ericovitchi a écrit:Moi j'essayerai par récurrence. C'est vrai pour n=1, suppose la relation vraie pour n et montre que c'est encore vrai pour n+1.
l'astuce sera d'écrire que
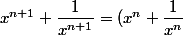(x+\dfrac{1}{x})-(x^{n-1}+\dfrac{1}{x^{n-1}}))
Et puis aussi que 4 cos(na) cos (a) - 2 cos((n-1)a) = 2cos((n+1)a) et on arrive au bout
C'est curieux.
Il me semble que dans le domaine réel, la relation x+1/x=2cos(a) implique
x=0, a=0 ou x=-1, a=pi

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Avr 2013, 22:07
par Ericovitchi » 18 Avr 2013, 22:07
hammana a écrit:C'est curieux.
Il me semble que dans le domaine réel, la relation x+1/x=2cos(a) implique
x=0, a=0 ou x=-1, a=pi
ha bon ? pourquoi dis-tu ça ?
x=0 avec un 1/x, ça métonnerait
-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 18 Avr 2013, 22:20
par hammana » 18 Avr 2013, 22:20
Ericovitchi a écrit:ha bon ? pourquoi dis-tu ça ?
x=0 avec un 1/x, ça métonnerait
si x=0, 1/x est infini !
la fonction x+1/x passe par un minimum=2 pour x=1, ou bien il y a quelque chose qui m'échappe
-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 18 Avr 2013, 22:28
par hammana » 18 Avr 2013, 22:28
Ericovitchi a écrit:ha bon ? pourquoi dis-tu ça ?
x=0 avec un 1/x, ça métonnerait
mes excuses. Je voulais écrire x=1, a=0 ou x=-1, a=pi

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Avr 2013, 15:01
par Ericovitchi » 19 Avr 2013, 15:01
hammana a écrit:mes excuses. Je voulais écrire x=1, a=0 ou x=-1, a=pi
Oui effectivement, en y réfléchissant, tu as raison, x+1/x est toujours supérieur à 2 (ou inférieur à -2) donc (x+1/x)/2 est supérieur ou égal à 1 (ou inférieur à -1) . Il ne peut valoir un cosinus que s'il vaut 1 ou -1 donc on a forcement cos a= 1 ou -1 donc a=0 ou pi et on en déduis x.
Ça hôte un peu d'intérêt à l'exercice. On peut donc directement démontrer la relation avec le n.
Cela dit, la démonstration par récurrence est valable quand même je pense.
-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 20 Avr 2013, 08:20
par hammana » 20 Avr 2013, 08:20
Ericovitchi a écrit:Oui effectivement, en y réfléchissant, tu as raison, x+1/x est toujours supérieur à 2 (ou inférieur à -2) donc (x+1/x)/2 est supérieur ou égal à 1 (ou inférieur à -1) . Il ne peut valoir un cosinus que s'il vaut 1 ou -1 donc on a forcement cos a= 1 ou -1 donc a=0 ou pi et on en déduis x.
Ça hôte un peu d'intérêt à l'exercice. On peut donc directement démontrer la relation avec le n.
Cela dit, la démonstration par récurrence est valable quand même je pense.
Le problème à l'origine devait supposer que x est un nombre complexe, en se restreignant au domaine réel il devient banal.
Ta démonstration est valable, mais il serait plus simple de rester dans le domaine complexe.
Si
+isin(a)),(1/x)=1/r(cos(a)-isin(a))
cos(a)+(r-1/r)sin(a)=2cos(a))
ce qui implique (r-1/r)=0 donc r=1. En appliquant la formule de Moivre:
+isin(na))
^n=cos(na)-isin(na))
d'où
^n=2cos(na)) Il est plus difficile de faire simple que de faire compliqué (Steve Jobs)
Il est plus difficile de faire simple que de faire compliqué (Steve Jobs)

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 20 Avr 2013, 13:23
par Ericovitchi » 20 Avr 2013, 13:23
oui effectivement, c'est plus naturel comme ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités