Exercice de logique

[Nivindina]

Bonjour à tous ! Alors voilà, je bloque à cet exercice figurant dans un concours de commerce. Le but étant de dire si chaque proposition est vraie ou non. J'ai essayé d'appliquer la formule de probas lorsque A et B sont indépendants mais ça ne marche pas.. Merci de votre aide.

Dans une école de commerce, la promotion de première année comprend 200 étudiants qui doivent pratiquer au moins l'une des 3 langues suivantes : anglais, allemand, espagnol. On sait que :
160 étudiants pratiquent l'anglais
120 étudiants pratiquent l'espagnol
60 étudiants pratiquent l'allemand

A partir de ces informations, on peut conclure que :
a) Si 30 étudiants pratiquent les 3 langue alors 80 étudiants pratiquent exactement 2 langues
b) Si 60 étudiants pratiquent seulement une langue alors aucun étudiant pratique les 3 langues
c) Le nombre d'étudiants pratiquant une seule langue est inférieur ou égal à 130
d) Plus de 180 étudiants pratiquent au moins l'une des 2 langues : allemand ou espagnol

[kelthuzad]

Salut,

Moi je le ferai comme ceci, soient :

x le nombre d'étudiants ayant pris 1 langue
y le nombre d'étudiants ayant pris 2 langues
z le nombre d'étudiants ayant pris 3 langues



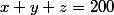
Et langues choisies, ainsi on peut noter :



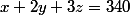
J'espère que c'est clair c'est la partie délicate. Car ensuite il suffit de rajouter la condition de l'énoncé a, b, c, d pour voir si l'affirmation est vraie, par exemple pour la a) on résout :

(un rappel : l'accolade montre qu'on a à faire à un système d'équations, cela signifie qu'on cherche les valeurs que peuvent prendre x, y et z pour que ces 3 lignes soient vraies, c'est en quel que sorte un "ET" pour chaque ligne)







Je remplace ici la deuxième ligne par elle-même moins la première :





Ici les 3 lignes de départ ne sont vraies que si x, y et z valent ces valeurs trouvées.
Autrement dit z = 30 implique y = 80. En français :
Si 30 ont choisi 3 langues alors forcément 80 ont choisi 2 langues suivant les conditions de l'énoncé. (et on s'en fout mais 90 ont choisi une langue)

[kelthuzad]

Pour le b)



Trouve-t-on ?

Pour le c) c'est un peu plus compliqué, on peut montrer que x appartient à [60, 130] mais je vais peut-être t'attendre.

[Nivindina]

Bonjour et merci pour votre réponse détaillée.
Mais je bloque dès le début.. Je comprends pas comment on peut déduire que x+2y+3z=340 en sachant que 160+120+60=340.
Car en supposant que x=60, 3z=180, alors qu'ici on a 160... :/

[Nivindina]

Et pour le b, je viens de résoudre l'inéquation, on trouve bien z=0.

[chan79]

Bonjour et merci pour votre réponse détaillée.
Mais je bloque dès le début.. Je comprends pas comment on peut déduire que x+2y+3z=340 en sachant que 160+120+60=340.
Car en supposant que x=60, 3z=180, alors qu'ici on a 160... :/

Si on ajoute le nombre d'étudiants en l'anglais, le nombre d'étudiants en allemand et le nombre d'étudiants en espagnol, on obtient:
d'une part 160+120+60=340
d'autre part le nombre total d'étudiants ( soit 200) + le nombre de ceux qui font exactement deux langues + 2 fois les 60 qui font les 3.
Le nombre cherché est 340-200-2*30=80

[Nivindina]

Si on ajoute le nombre d'étudiants en l'anglais, le nombre d'étudiants en allemand et le nombre d'étudiants en espagnol, on obtient:
d'une part 160+120+60=340
d'autre part le nombre total d'étudiants ( soit 200) + le nombre de ceux qui font exactement deux langues + 2 fois les 60 qui font les 3.
Le nombre cherché est 340-200-2*30=80

Effectivement, cela donne bien 80, et je comprend ce calcul.
Cependant ma question est de savoir pourquoi vous prenez "2 fois les 30 qui font 3" ? Pourquoi ne pas seulement prendre les 30 ? Pourquoi le multiplier par 2 ? Et pourquoi multiplier le nombre de ceux qui ont pris 3 langues par 3?
Ce qui revient à demander d'où viennent les coefficients dans l'équation x+2y+3y=340.

[chan79]

Effectivement, cela donne bien 80, et je comprend ce calcul.
Cependant ma question est de savoir pourquoi vous prenez "2 fois les 30 qui font 3" ? Pourquoi ne pas seulement prendre les 30 ? Pourquoi le multiplier par 2 ? Et pourquoi multiplier le nombre de ceux qui ont pris 3 langues par 3?
Ce qui revient à demander d'où viennent les coefficients dans l'équation x+2y+3y=340.

Dans les 340, ceux qui font une seule langue sont comptés 1 fois, ceux qui font exactement deux langues sont comptés deux fois et ceux qui font les langues sont comptés trois fois.
Si on retranche les 200 aux 340, il reste ceux qui font deux langues comptés une fois et ceux qui font les trois comptés deux fois.
D'où le calcul 340-200-2*30=80
Sinon, bien-sûr, on utilise les inconnues comme proposé ci-dessus.(c'est peut-être incontournable pour les questions suivantes)

[chan79]

Pour le c,
x+y+z=200
x+2y+3z=340
Passe les x à droite
Résous le système en calculant y et z en fonction de x
y et z doivent être positifs ...

[chan79]

contre-exemple pour le d

[Nivindina]

Merci beaucoup ! J'ai (enfin) compris. :)