Exercice limites d'une suite

[Evodie]

Bonjour, pouvez vous m'aidez à faire ce petit exo en urgence, svp.. le voici :
Soit la suite (Un) définie pour tout entier naturel par : Un=3n^2+4n-1
=> Vérifier que lim Un = +oo lorsque n tend vers +oo.
Je ne sais pas comment procéder, merci d'avance :)

[Evodie]

les lois des limites ? euh raisonnement par récurrence ?

[Evodie]

=> lim 3n^2 = +oo
=> lim 4n = +oo
Donc par somme, limite de Un est +oo

C'est juste ?

[Anonyme]

OUI c'est correct

Exercice un plus difficile
Calculer la limite quand n tend vers en +infini de

[Evodie]

Euh rapidement, pouvez vous vérifier ceci svp ?

*On a : Un = lim ;)(2x^2-2x+3)/x avec x qui tend vers +oo
=> lim ;)(2x^2-2x+3)=3
=> lim x= +oo

Donc, par quotient, lim Un= 0 lorsque x tend vers +oo

*On a : f(x)= lim sin(x+pi) / x lorsque x tend vers O
=> lim x+pi = pi, d'où : sin (x+pi) tend vers l quand x tend vers x
=> lim x = 0 en restant positif
Donc lim f(x)= +oo lorsque x tend vers 0

Est-ce correct ?


Merci pour vos réponses, et concernant l'exercice que tu m'a proposé Ptitnoir, je suis intéressé, seulement aujourd'hui je suis trop occupé, mais je le ferai dès que possible, :D

[Anonyme]

Ce n'est pas une suite car l'expression (2x^2-2x+3)/x ne dépend pas de n

Si on pose , on peut calculer la limite de la fonction f quand x tend vers +infini

Si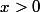 alors
et donc il est facile de calculer cette limite


Remarque 1
Concernant la limite de quand x tend vers 0
cela donne une Forme Indéterminée (FI : 0/0)
As tu une idée pour résoudre cette FI ?

Remarque 2 : concernant mon exercice
la limite de cette suite quand n tend vers +infini donne une Forme indéterminée (FI : +infini - infini)
As tu une idée pour résoudre cette FI ?

[Evodie]

Oh oui désolé ce n'était même pas marqué dans l'énoncé que c'était une suite...

[Evodie]

Pour résoudre l'FI de votre exercice, il faut faire une factorisation par le plus haut terme, ici n^2 ?

Sinon je pense que pour mon exercice, il faudrait aussi faire une factorisation

[Anonyme]

Pour résoudre l'FI de votre exercice, il faut faire une factorisation par le plus haut terme, ici n^2 ?

OUI

Concernant la FI 0/0 pour le calcul de la limite de quand x tend vers 0

Pour résoudre cette FI il faut faire apparaitre le taux de variation de la fonction sinus sur un intervalle qui contient 0

Je commence (et tu finiras) le raisonnement



C'est le taux de variation de la fonction sinus entre x et 0 (avec un signe - devant)
Quelle est la la limite de cette expression quand x tend vers 0 ? ( voir le chapitre "dérivation de fonction")

[Evodie]

Pour résoudre l'FI de votre exercice, il faut faire une factorisation par le plus haut terme, ici n^2 ?

Sinon je pense que pour mon exercice, il faudrait aussi faire une factorisation

Désolé mais je ne sais pas comment résoudre l'FI de mon exercice..

[Anonyme]

As tu compris mon post précédent ou est une autre fonction (et une autre FI ) ?

Explique quels sont tes problèmes

[Evodie]

En fait je suis en train de me préparer à aller à l'école et je n'ai plus le temps de réfléchir correctement, c'est pourquoi je ne comprend plus rien

[Anonyme]

En fait je suis en train de me préparer à aller à l'école et je n'ai plus le temps de réfléchir correctement, c'est pourquoi je ne comprend plus rien

Prends ton temps et reviens sur ce forum en relisant cette discussion à tête reposé...
Courage dans moins d'un mois c'est les vacances (15 jours !)

[Evodie]

OUI c'est correct

Exercice un plus difficile
Calculer la limite quand n tend vers en +infini de

Alors :
=> lim 3n^2 = +oo
=> lim -4n = -oo
C'est une FI

Or pour tout n>0, Un= n^2(3-(4n/n^2)-n^2)
=> lim n^2 = +oo
=> lim -(4n/n^2)=-oo, d'où, par somme, lim [n->+oo] (3-(4n/n^2)-n^2) = -oo

Donc par quotient, lim [n->+oo] Un = -oo


Voilà

... Par contre pour mon exercice je bloque xD

[Anonyme]

@Evodie
Tu as fait une erreur dans la factorisation par

On a :

et donc la limite de est quand n tend vers +infini

Concernant ton exercice, je te conseille de relire les explications que je t'ai donné et qui expliquent l'utilisation du taux de variation de la fonction sinus entre 0 et x ( pour résoudre la FI 0/0 )

Et si tu rencontres des difficultés pour comprendre, peux tu, poser des questions plus précises que "je ne comprends pas", sinon je ne sais pas quoi t'expliquer d'autre....