Exercice limites de fonctions

[tomtom21]

Bonjour, j'ai un exercice sur des limites à faire mais je coince sur certains points...

Voici l'énoncé et les questions :
Etude du comportement de cos(x) en

1/ Si l'on suppose que cos(x) admet une limite en , expliquer pourquoi cette limite ne peut être infinie.

J'ai répondu : La limite ne peut pas être infinie vu que .
Car n'a pas de limite, vu que la fonction f(x) = cos(x) oscille dans l'intervalle [-1;1] en

2/ On suppose que

- On considère la suite
Donner

J'ai répondu :

- En calculant de deux façons différentes , démontrer que la limite est égale à 1.

C'est là que je coince !
J'ai pensé à utiliser comme première méthode de calcul en posant : et
Mais je n'arrive pas du tout à arriver à une limite de 1...

Un peu d'aide svp ?

[sxmwoody]

Bonjour, j'ai un exercice sur des limites à faire mais je coince sur certains points...

Voici l'énoncé et les questions :
Etude du comportement de cos(x) en

1/ Si l'on suppose que cos(x) admet une limite en , expliquer pourquoi cette limite ne peut être infinie.

J'ai répondu : La limite ne peut pas être infinie vu que .
Car n'a pas de limite, vu que la fonction f(x) = cos(x) oscille dans l'intervalle [-1;1] en

2/ On suppose que

- On considère la suite
Donner

J'ai répondu :

- En calculant de deux façons différentes , démontrer que la limite est égale à 1.

C'est là que je coince !
J'ai pensé à utiliser comme première méthode de calcul en posant : et
Mais je n'arrive pas du tout à arriver à une limite de 1...

Un peu d'aide svp ?

[QUOTE sxmwoody] bonjour...en terminale on apprend que {-1}\leq{\cosx}{\leq}{+1 }[/quote] la fonction étant périodique ses bornes sont donc -1 et +1 à {pm}{\inf}
previsualisation réponse ???

[masque gazé]

Salut

Cette exercice est une démonstration des limites de cos
tu va donc chercher dans cette exercice les limites de cos


1/ Si l'on suppose que cos(x) admet une limite en , expliquer pourquoi cette limite ne peut être infinie.

J'ai répondu : La limite ne peut pas être infinie vu que .
Car n'a pas de limite, vu que la fonction f(x) = cos(x) oscille dans l'intervalle [-1;1] en

===========================================================

Dire que cos n'a pas de limite, c'est contredire l'énoncé et ça c'est pas bien.
Le but de cette exercice est justement de démontrer les limites de cos.
Si tente de résoudre cette exercice en te disant en permanence tes réponses ne seront pas correctes.

Parcontre dire que cos : suffit pour dire que la soit disant limite de cos est finie


===========================================================

2/ On suppose que

- On considère la suite
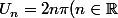Donner

J'ai répondu :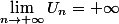

===========================================================

Là je suis d'accord avec toi.

===========================================================

- En calculant de deux façons différentes , démontrer que la limite est égale à 1.

===========================================================
cos(2)=1
cos(2n)=1

Donc cos(Un)=1

Voilà, et la deuxième méthode... à froid, je ne vois pas de suite. :lol3:

[tomtom21]

Bonsoir, merci pour ta réponse claire et rapide ! :++:

Je vais essayer de voir si je trouve quelque chose également de mon côté pour la deuxième manière de calculer la limite.

Sinon je passerai à la dernière question (que je n'ai pas encore mentionné dans ce topic).

Encore merci et bonne soirée ! :lol2:

[masque gazé]

Sinon pour la deuxième méthode:



Donc

[Ben314]

Salut,
La "soit-disant" deuxième méthode, ben ça consiste bêtement à dire que, vu que et qu'on a supposé que alors .
Et on en déduit que

et dans la partie suivante on va surement montrer que en considérant

[tomtom21]

Bonjour tout le monde,

merci pour vos nombreuses réponses.

Et oui du coup la prochaine question est :

"En reprenant la question précédente, avec la suite


Aboutir à une contradiction et conclure sur le comportement de la fonction en

[NOVICE76]

Bonjour tout le monde,

merci pour vos nombreuses réponses.

Et oui du coup la prochaine question est :

"En reprenant la question précédente, avec la suite


Aboutir à une contradiction et conclure sur le comportement de la fonction en

En quelle classe est tu ?
1er ou terminale
la réponse n'est pas la même

[tomtom21]

Je suis en terminale S.

Et oui j'avais remarqué à propos des réponses.

[NOVICE76]

Je suis en terminale S.

Et oui j'avais remarqué à propos des réponses.

Dans ce cas on utilise le théorèmes des gendarmes par encadrement de la limite.
COS X ne peut varier qu'entre - 1 et + 1
donc - 1 < Lim COS X < +1

[NOVICE76]

[quote="NOVICE76"]Dans ce cas on utilise le théorèmes des gendarmes par encadrement de la limite.
COS X ne peut varier qu'entre - 1 et + 1
donc - 1 infini = infini